PROJECTIVE GEOMETRY COURSE
Chapter 2: PROJECTIVE MAPPINGS FROM A LINE ONTO A LINE
§ 8: Perspectivities and projectivities
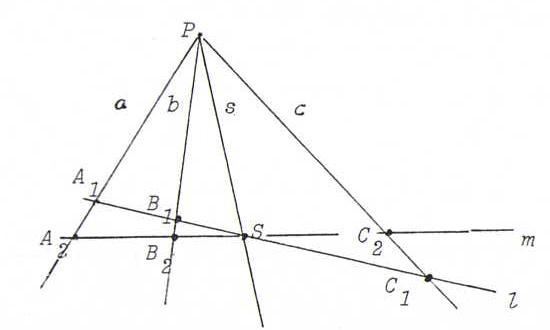
Let l and m be two lines in the real projective plane, and let P be a point, not on l and not on m.
By projection from P we get a bijection from l onto m whose intersection point l.m is a fixed point.

We call this bijection a perspectivity, and use the formula l(A1,B1,S,C1) ∧=P
m(A2,B2,S,C2).
We call P the perspectivity center of this perspectivity.
We have at the same time a bijection from (the pencil of lines through) P onto (the pencil of points on) l which we call elementary perspectivity of intersection:
P(a,b,s,c,...) ∧= l(A1,B1,S,C1,...).
We call the inverse mapping an elementary perspectivity of connection.
So the perspectivity from l onto m with center P is the product of the perspectivity of connection from l to P and the perspectivity of intersection from P
to m.
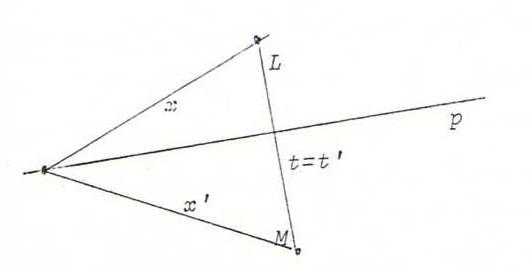
Now the dual case: start from two points L and M and a line p not going through L or M.
The product of the elementary perspectivity of intersection from L to p and the elementary perspectivity of connection from p to M is a bijection from L to
M, which we call perspectivity with axis p.
The line LM is invariant. We write L(x,t,...) ∧=p M(x',t',...), etc.
We call the composition of one or more (elementary) perspectivities a projectivity.
So we distinguish projectivities between ( the pencils of points on) two lines, projectivities between (the pencils of lines through) two points, projectivities between a line and a point,
and projectivities between a point and a line. An example:
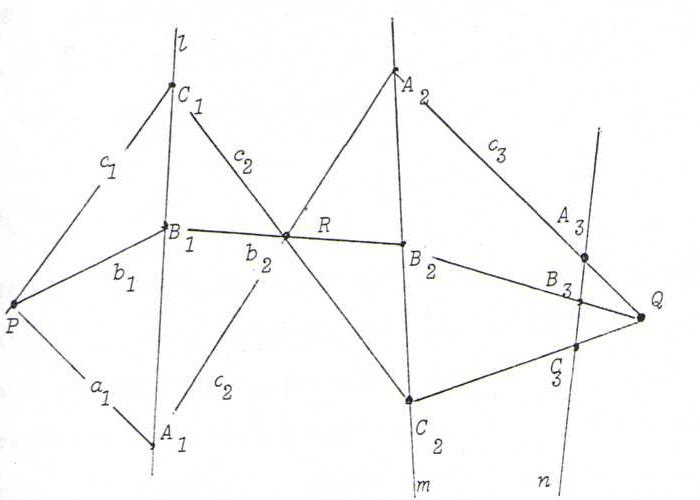
Notations l(A1,B1,C1,...) ∧- m(A2,B2,C2,...),
P(a1,b1,c1,...) ∧- Q(a3,b3,c3,...),
P(a1,b1,c1,...) ∧- n(A3,B3,C3,...), etc.
This last formula means: "There exists a projectivity from P onto n that maps a1 to A3, b1 to B3, and
c1 to C3."
As an exercise, take an arbitrary point X1 on l, and construct the image point X2 under the first of the three projectivities denoted by
the formulas below the picture.
Let x1:=PX1, and construct the image x3 under the second projectivity, and also the image X3 under the third.
The mapping X1 → x3.l is a projectivity from l onto l. (We call the pencils of points {X1} and {x3.l}
superposed pencils of points in a projective correspondence. Likewise we can construct superposed pencils of lines in a projective correspondence.)
Nota bene: formulas like l(A,B,C) ∧= m(A',B',C') denote assertions (in this case: "there exists a perspectivity from
l onto m that maps A to A', B to B', and C to C' ").
When A, B, C, D lie on l, and E, F, G, H on m, the assertions l(A) ∧= m(E) and
l(A,B) ∧= m(E,F) are always true, but l(A,B,C) ∧= m(E,F,G) only if
CG goes through the intersection point of AE and BF;
the assertions l(A) ∧- m(E) , l(A,B) ∧- m(E,F) , and even
l(A,B,C) ∧- m(E,F,G) (see O34) are always true, but
l(A,B,C,D) ∧- m(E,F,G,H) is only true if H has a special position with respect to the other seven points.
O32 Let r be a line, and let R∞ be the point at infinity of that line. Let A, B and I be distinct points on r, not equal to
R∞, and P a proper point not on r.
Project the given points from P onto a line r' (going through I and not coinciding with r, with point at infinity R∞).
Also project R∞ onto r' and R∞ onto r.
O33 Choose three distinct points A, B and C on a line l. Let P be a point outside l, and m a line through A but not through P.
Project A, B, C from P onto m and find image points A', B', C'. Let Q be the intersection point B'C.BC'.
Show that there exists a projectivity satisfying l(A,B,C) ∧- l(A,C,B).
Make the dual construction, too.
O34 Let A, B, C be three distinct points on a line l and A', B', C' three distinct points on a line m.
Prove that there exists at least one projectivity that maps A, B and C to (respectively) A', B' and C'.
Distinguish three cases.