§ 8: answers

O32

O33

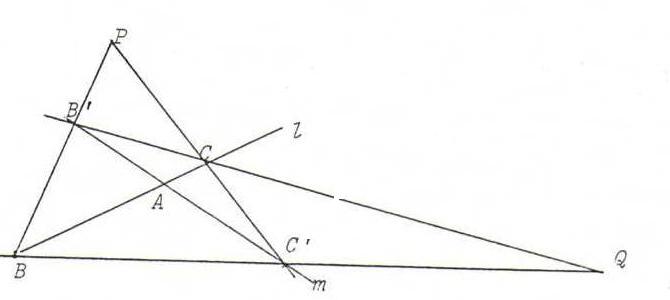
l(A,B,C) _∧=^Q m(A,C',B') _∧=^P l(A,C,B)

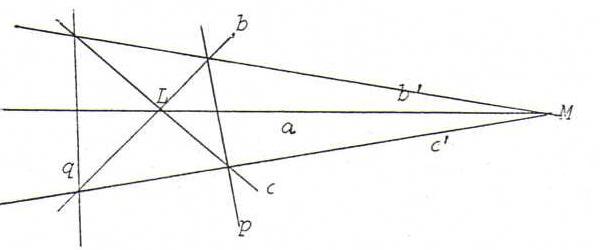
L(a,b,c) _∧=^q M(a,c',b') _∧=^p L(a,c,b)

O34

i) A=A'. Then we can take the perspectivity from l onto m with center BB'.CC'.

ii) The six points are distinct and l ≠ m. See the drawing.

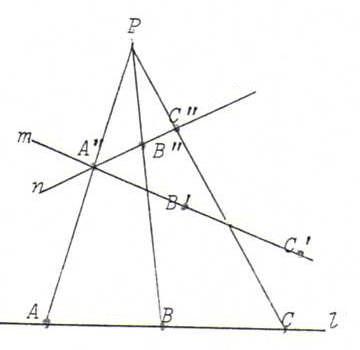
Choose n through A' and P on AA'.
B" and C" are the projections of B and C from P on n.
Then we can take the composition φoψ where ψ is the perspectivity from l onto n with center P, and φ the perspectivity from n onto m with center B'B".C'C".

iii) The six points are lying on one line, so l=m.

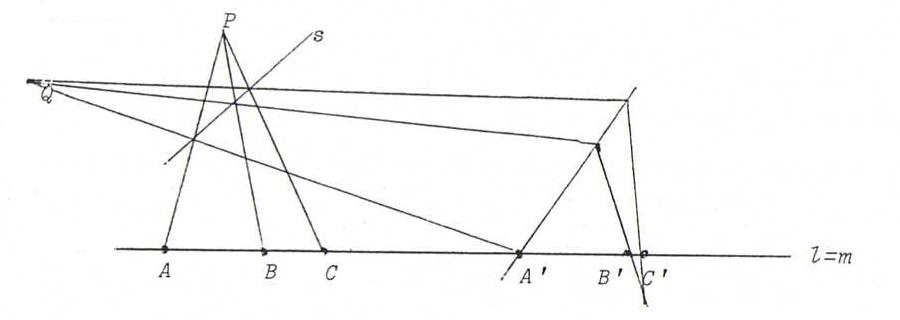
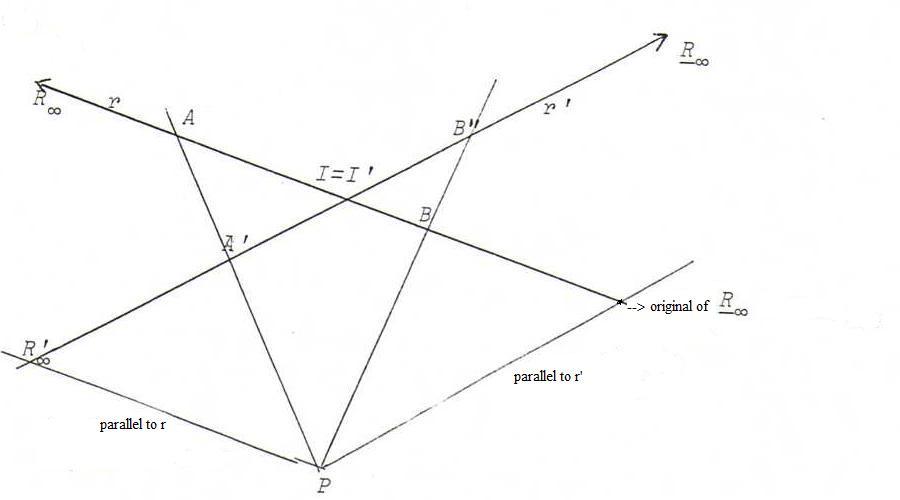
Study the picture above and show we can take a projectivity that is the product of three perspectivities.