The American Mathematical Monthly shows the problems of the issues from the years 1894 through 1922 free of charge, so I tried some of them.
7 miscellaneous, reverend Gridley (From the second issue of 1894)
Making no allowance for the curvature of the earth, and supposing the sun to rise in the east and set in the west, what would be the course of a man who should walk constantly toward the sun
from morning until night? How far and in what direction from the starting point would he be, walking three miles per hour, at the end of three days?
Partial solution:
In fact it's easier to allow for the earth's spherical curvature, if only we let the man walk on the equator on a day that runs from 6 o'clock in the morning to 6 o'clock in the evening, starting at noon
of the first day.
It turns out the man walks 0.0432 degrees per hour and the sun turns 15 degrees per hour.
The man and the sun first meet after t1 hours at position x1 degrees where x1 = t1*0.0432 = 90 - 15*t1, so t1 = 5.98277 hours,
x1 = 0.25845565 degrees.
The rest of the first day, during t2 = 0.01723 hours, the man follows the sun, walking over 0.01723*0.0432 = 0.000744 degrees to position x2 = 0.25845565 - 0.000744 = 0.25771165 degrees.
Next morning, the man and the sun meet after t3 hours at position x3 degrees where x3 = x2 + 0.0432*t3 = 90 - 15*t3, so
t3 = 5.965638 hours, and x3 = 0.515427 degrees. The rest of the second day, during t4 = 12 - 5.965638 = 6.034362 hours, the man follows the sun, walking over ... (etc.).
12 diophantine equations (From the May issue of 1894)
Find positive integers a,b,c such that the som of their squares is a cube and the sum of their cubes is a square.
Partial solution:
Using a Pascal program, I found 3,3,3 and 192,192,192 and 252,234,198 and 464,304,256.
Moreover, if a,b,c is a solution, then, for any positive integer m,
m6a,m6b,m6c is a solution, too.
(AMM gives more solutions.)
14 geometry (From the very first issue of 1894) Through a given point to draw four circles tangent to two given circles.
Sketch of a solution:
Let the given point be (0,0). Let the center and radius of one of the given circles be (a,b) and r, and those of the other (d,e) and s.
We seek a circle with center (u,v) and radius t = √(u2+v2) which is tangent to both given circles.
In any case this amounts to √((u-a)2+(v-b)2) = ± (r ± t) and √((u-d)2+(v-e)2) = ± (r ± s) for certain values of ±.
Using (u,v) = p(cos(t),sin(t)) we find:
2ap cos(t) + 2bp sin(t) = a2+b2-r2±2rp and 2dp cos(t) + 2ep sin(t) = d2+e2-s2±2sp.
Solving for cos(t) and sin(t), and using sin2(t) + cos2(t) = 1, we find in the end four values of (p,cos(t),sin(t)) which may be constructed with compass and straightedge.
This reasoning may be extended to: 13 Through a given point to pass four spherical surfaces tangent to two given spheres.
15 calculus From a given quantity of material a cylindrical cup with circular bottom and open top is to be made, the cup to contain the greatest amount. What must be its dimensions?
Solution:
Denote by g the volume of the material, by d the thickness of cylinder and bottom, by r the radius of the circular bottom inside the cup, and by h the height of the cylinder inside the cup.
Then we have the restriction g = πr2d + 2πrhd, or r2 + 2rh = a for a:=g/(πd), so h = (a - r2)/(2r).
Now we must maximize the contents of the cup, that is hπr2 = (π/2)(ar - r3).
With (d/dr)(ar - r3) = 0 we find r = √(a/3) and then, using the restriction, h = r.
16 diophantine equations (september 1894)
Find three numbers (x,y,z) such that the sum of the cube of any one of the three and the squares of the other two
will be a square.
Partial solution:
We find all solutions with x = y = z from x3+2x2 = x2(x+2) = square,
so x = m2-2. So we have (x,y,z) = (m2-2,m2-2,m2-2) for all m greater than 1.
I found all other solutions with x,y,z at most 1000 with the help of a pascal program: (9,324,324), (54,54,414), (97,776,776).
(AMM gives only (2,2,2).)
17 average and probability (from the August issue of 1894)
Given a circle with radius 1, what is the average area enclosed by the midpoints of chords that pass through
a random point within the given circle?
Solution:
For the random point we may take (0,r). Then the midpoints of the chords form a circle with center (0,r/2) and
radius r/2.
So the mean area asked for is ∫01 πr2/4 = π/12.
17 geometry Draw a circle bisecting the circumferences of three given circles.
Correction:
This isn't always possible.
Give coordinates in such a way that the given circles have equations x2 + y2 = 1, (x-a)2 + (y-b)2 = r2, (x-c)2 + (y-d)2 = s2
and so that the circle we seek passes through (-1,0) and (1,0) and has equation x2 + (y-q)2 = 1 + q2.
There must exist some φ such that both (a + r cos(φ),b + r sin(φ)) and (a -r cos(φ),b - r sin(φ)) lie on x2 + (y-q)2 = 1 + q2,
and some ψ such that both (c + s cos(ψ),d + s sin(ψ)) and (c - s cos(ψ),d - s sin(ψ)) lie on x2 + (y-q)2 = 1 + q2.
It follows that q = (a2 + b2 + r2 - 1)/(2b) = (c2 + d2 + s2 - 1)/(2d),
and the latter equality is imposing a restriction on the given circles.
19 geometry If any point be taken on the circumference of a circle, and lines be drawn from it to the angles of an inscribed equilateral triangle, prove that the middle line so drawn is equal to the sum of the other two.
Solution:
Give coordinates in such a way that the arbitrary point is P(cos(t),sin(t)) for some t between 0 and π/2, and the angles are at A(1,0), B(-1/2,√3/2), C(-1/2,-√3/2).
It is straightforward to check that PB = PA + PC.
19 calculus A and B are in a circular room 30 feet in diameter, A being at the center and B at the circumference.
B runs around at the rate of 600 feet per minute, and A pursues him at the rate of 100 feet per minute.
How long will the race last and how far will each have traveled till B is caught.
Solution:
Since B is so good as to stay running along the circumference with constant speed, so b(t) = 15(cos(40t),sin(40t)), A has to be so flexible as to run straight to the correct point 15(cos(s),sin(s)) at the circumference, where he will catch B after 15/100 minutes. So the correct s is 40*15/100 = 6 radians.
If, however, A keeps obstinately running in the direction of B, we have a(t) = (x(t),y(t)) and find x(t) and y(t)
using a' ~ b-a and ||a'|| = 100.
I ran the following Pascal program:
program amm;
var p,x,y,t,dx,dy,dt:real;
begin
readln(dt);
t:=0;x:=0;y:=0;
while ((x*x+y*y)<225) do
begin
p:=(15*sin(40*t)-y)/(15*cos(40*t)-x);
dx:=100*dt/sqrt(p*p+1);dy:=p*dx;
t:=t+dt;x:=x+dx;y:=y+dy;
end;
writeln(t:13:10);readln
end.
I got output 0.2336512 minutes for input dt=0.0000001
So in the obstinate way A needs more than 150 percent of the time he needs in the flexible way.
19 miscellaneous (sept 1894) A spherical shell moving in a horizontal direction with constant velocity 1500 feet/sec
at uniform height g/2 feet explodes equally scattering the inclosed fragments with velocity 1200 feet/sec.
Draw the curve on the earth where the fragments fall.
Solution:
Since g is the constant of gravity, the fragments fall after 1 second.
So the curve is the circle (x,y) = (1200*cos(t) - 1500, 1200*sin(t)).
23 calculus (From the July issue of 1894)
From a point O situated in the plane of a plane curve, radii vectors are drawn to different points of the curve,
and on each one a distance is laid off from O inversely proportional to the length of the radius vector.
To determine the tangent at any point of the locus of the points thus obtained.
Solution:
Let the original curve be parametrized with polar coordinates r(cos(φ),sin(φ) and the derived curve
(cos(φ),sin(φ)/r.
The tangent vectors have the directions of, respectively,
(r'cos(φ)-rφ'sin(φ),r'sin(φ)+rφ'cos(φ)) and
(-r'cos(φ)-rφ'sin(φ),-r'sin(φ)+rφ'cos(φ)).
Then the cosinuses of the angles between (cos(φ),sin(φ)) and these tangent vectors are opposite,
so these angles are supplementary.
24 calculus (From the July issue of 1894)
At the president's reception, the citizens are admitted at 12:30, but the line begins to form at 11 in front of
the gate. By the time the doors are opened, there are in line 5400 people, who have gathered at a rate per second
proportional to the time after 11. The president is able to receive them at the rate of 45 per minute (clearly
not per second).
At what time should a person have joined the line to get through with the least delay?
Solution:
The rate of gatherers at t seconds after 11 is At, where ∫05400 At dt = 5400, so A = 1/2700.
If a person arrives after T seconds, there are ∫0T At dt = AT2/2
persons before him in the line,
so his waiting time until the president sees him is 5400 - T + 2AT2/3 seconds.
This is minimal iff T = 3/(4A) = 2025, so at 11:33:45.
25 algebra (From the June issue of 1894)
A man and a boy get n dollars for digging potatoes. The man can dig them as fast as the boy can pull the vines,
but the man can pull vines m times as fast as the boy can dig them. Divide the money.
Solution:
Suppose the man does p vines and the boy q vines, and the man needs s seconds to pull and t to dig, so
p(s+t) = q(t+ms).
Then the man gets np/(p+q) = n(ms+t)/((m+1)s+2t) and the boy nq/(p+q) = n(s+t)/((m+1)s+2t).
(If s=t, these portions are (m+1)n/(m+3) and 2n/(m+3); if, moreover, m=1.1 they are 21n/41 and 20n/41.)
25 diophantine equations (january 1895)
For a rectangular parallelopiped (shoebox) with side lengths a,b,d, face diagonals c,e,f, and
body diagonal g, try to make as many of these seven measurements integral as possible, using:
a2 + b2 = c2, a2 + d2 = e2,
b2 + d2 = f2, a2 + f2 = g2,
b2 + e2 = g2,
d2 + c2 = g2, c2 + e2 = f2.
Partial solution:
The last one of these seven equations, involving the three face diagonals, clearly never holds. The fifth and sixth
equation can be derived from the first four equations.
But I think with the fourth we can't ever find an integral body diagonal g if the first six measurements a,b,d,c,e,f
are integral and the first three equations hold.
The first three equations, each involving two side lengths and one face diaginal, are equivalent to
a2 = (c2 + e2 - f2)/2,
b2 = (c2 + f2 - e2)/2,
d2 = (e2 + f2 - c2)/2.
After extensive search with a Pascal program, I didn't find six positive integers a,b,d,c,e,f, each smaller than 1000, that
satisfy all three equations.
However, for the couple of the first two equations (a2 + b2 = c2,
a2 + d2 = e2), we easily find many integral solutions a,b,c,d,e:
Let a = k(p2 - q2), d = 2kpq, e = k(p2 + q2) for arbitrary numbers
k,p,q, so the second equation holds.
Furthermore, for a2 = (k(p2 - q2))2 we can easily find another
factorization a2 = uv = (c - b)(c + b) with c = (u+v)/2, b= (u-v)/2, so the first equation holds, too.
For example, this way, with k,p,q = 15,6,3, I found a,d,e,c,b = 405,540,675,477,252.
27 calculus (september 1894)
A runs around the circumference of a circular field (radius R feet) with velocity m feet/sec. B starts from the
center with velocity n > m to catch A. The straight line joining their positions always passes through the center.
Find the equation of the curve described by B, the distance he runs, and the time occupied.
Solution:
The positions of A and B at time t are a(t) = R(cos(mt/R),sin(mt/R), b(t) = Rr(t)(cos(mt/R),sin(mt/R),
where n2 = ||b'||2 = (Rr')2 + (mr)2.
So t = ∫0r(t) R/√(n2-(mρ)2)) dρ =(R/m)arcsin(mr(t)/n).
Hence the total time occupied is T = (R/m)arcsin(m/n), the distance run is R*arcsin(m/n) and b(t) is
described as above with r(t) = (n/m)sin(mt/R).
29 calculus (october 1894)
A hen runs around the circumference of a circular field (radius 50 feet) with velocity 2 feet/sec.
A hawk starts from 600 feet above the center of the field with velocity 5 feet/sec to catch the hen.
The straight line joining their positions always passes through the starting position of the hawk.
Find the equation of the curve described by the hawk, the distance he flies, and the time occupied.
Criticism and solutions:
We can find an analytic solution like in problem 27 calculus above.
However, it's not realistic to assume the hawk always stays on the line from his starting position to the running hen.
In fact, he just flies in the direction of the hen and doesn't mind what's behind him.
Now the equations are a bit more complicated, but we can find a numerical solution
like in problem 19 calculus above.
Let k = (50 cos(t/25), 50 sin(t/25),0) be the position of the hen at time t, and h = (x(t),y(t),z(t)) the position of the hawk, with (x(0),y(0),z(0)) = (0,0,600).
In the problem as stated by AMM, we have h = (x,y,z) = (0,0,600) + λ(t)(50 cos(t/25), 50 sin(t/25),-600).
We have to find λ(t) with λ(0) = 0, using ||(x',y',z')|| = 5.
Then we find the time T the hawk needs from λ(T) = 1, and the distance he flies from S=5T.
We get λ = (5/2)*sin(t/(25√145)) and T = 123.88 sec.
In the realistic version, the formulas with λ don't hold.
Instead, we use (x',y',z') ~ (50 cos(t/25) - x, 50 sin(t/25) - y, - z) and ||(x',y',z')|| = 5.
I ran the following pascal program and found T = 126.684 seconds.
program amm;
var x,y,z,t,dx,dy,dz,dt,p,q:real;
begin
x:=0;y:=0;z:=600;t:=0;dt:=0.001;
while z>0 do
begin
p:=(x-50*cos(t/25))/z;q:=(y-50*sin(t/25))/z;
dz:=-5*dt/sqrt(1+p*p+q*q);
dx:=p*dz;dy:=q*dz;
x:=x+dx;y:=y+dy;z:=z+dz;
t:=t+dt
end;
writeln(t:13:3);readln
end.
39 diophantine analysis (september 1895)
The m-th root of the n-th power of an integral number is a perfect p-th power. What is that number?
Solution:
Let x = p1a1 ... pkak be the prime power factorization of an arbitrary positive
integer.
Then x satisfies the conditions iff there exist natural numbers b1, ... , bk ,
such that for i = 1, ..., k holds nai = pmbi.
So let q be the least common multiple of n and pm. Then we get all positive solutions x by taking
ai = (q/n)ci and bi = (q/(pm))ci for arbitrary natural numbers
c1, ... , ck.
39 average and probability (june 1896)
A man is at the center of a circular desert. He travels at a given rate, but in a perfectly random manner.
What is the probability that he will be off the desert in a given time?
Criticism and partial solution:
I suppose the desert has a radius of 100 km and the man is a perfect robot who steps 1 meter in a random direction every second.
I wrote and ran a pascal program and found he is off the desert after 11410471109 seconds, which is almost 362 years.
The program listing is as follows:
program amm;
const pi=3.1415926536;
var x,y,f,m,n:real;
begin
x:=0;y:=0;m:=0;n:=0;
while m<100000 do
begin
n:=n+1;f:=random*2*pi;
x:=x+cos(f);y:=y+sin(f);
if sqrt(x*x+y*y)>m then
begin
m:=sqrt(x*x+y*y);writeln(n:13:0,m:13:6)
end
end;readln
end.
46 average and probability (november 1896)
Four men starting from random points on the circumference of a circular field and traveling at different rates
take random straight courses across it. Find the chance that at least two of them will meet.
Criticism and solution:
If the four men travel at different rates they surely won't meet.
However, there's a positive chance at least two of the courses intersect.
Indeed, there are 7! = 5040 distinct possible orders of the 8 endpoints of the courses and 64 of them belong to
courses that don't intersect. So the chance that at least two of the courses intersect is 311/315.
50 calculus (December 1895)
A drawbridge, F feet in length, moves uniformly about a center axis. At the instant it began to open, a man
stepped on the end; and, walking at a uniform rate in the straight line passing through its center, reached the opposite
end just as it made N complete revolutions. Find the absolute path described by the man, and the ratio of his rate of
motion in this path and the velocity of the end of the bridge. Apply the result to the case when F=320 and N=2.
Solution:
Let t ∈ [0,N] be the time measured in such a way that at t = 1 the bridge has completed 1 revolution.
If the bridge would not move, the man would walk from (0,F/2) to (0,-F/2), and his position at time t would be
(0,F*(N-2t)/(2N)).
In reality, the bridge performs a rotation with matrix D, where D1,1 = cos(2πt),
D1,2 = -sin(2πt), D2,1 = sin(2πt), D2,2 = cos(2πt),
so the position of the man at time t is (x,y) = F*((N-2t)/(2N))*(-sin(2πt),cos(2πt)).
The rate of motion of the man is the length of the derivative:
(x',y') = a*(-sin(2πt),cos(2πt)) +
b*(-cos(2πt),-sin(2πt)), where a = F*(-1/N) and b = F*((N-2t)/(2N))*2π.
This length is √(a2 + b2) = (F/N)*√(1 + π2(2t-N)2).
The position of the end of the bridge at time t is (F/2)*(-sin(2πt),cos(2πt)), whose derivative has lenght πF.
So the ratio asked for is (1/(πN))*√(1 + π2(2t-N)2), independent of F.
For N=2 we get (1/(2π))*√(1 + 4π2(t-1)2).
If the man had stayed at the end of the bridge, he would have been at the other side of the canal at t = 1/2.
And he wouldn't have been dizzy.
54 algebra (July 1895)
Write as a product: x2 + y2 + z2 - 2xy - 2xz - 2yz.
Solution:
I tried (ax + by + cz + d√(xy) + e√(xz) + f√(yz))
(gx + hy + iz + j√(xy) + k√(xz) + l√(yz)).
But then I saw it's even simpler:(x - y - z)2 - 4yz = (x - y - z - 2√(yz))(x - y - z + 2√(yz))
Isolated problem (may 1896)
What is the locus of the points from which any two segments in space, AB and CD, appear under the same constant angle?
Partial solution:
If the cosine of the angel is p with 0 < p < 1, the locus is the intersection of two fourth-degree surfaces with
equations
((x1-a1)(x1-b1)+(x2-a2)(x2-b2)+
(x3-a3)(x3-b3))/(√((x1-a1)2+
(x2-a2)2+(x3-a3)2)*
√((x1-b1)2+
(x2-b2)2+(x3-b3)2)) = p, and the same equation with c and d
instead of a and b. I don't know whether we can specify the surfaces more exactly with geometry.
In the case when p = 0 (so the angle is 90 degrees), we get the equations of two spheres with diameters AB and CD, respectively, which is clearly accurate in view of the theorem of Thales. If the spheres have more than 1 points in common, the intersection is a circle.
59 average and probability (january 1898)
A circle is rolling along a horizontal straight line. The uniform velocity of the center is v.
Find the average velocity of a point on the circle.
Solution:
The point on the circle is after t seconds in x = (vt - r sin(vt/r), r - r cos(vt/r)).
Its velocity is the length of the derivative, which is 2v sin(vt/(2r)).
So its average velocity is 4v/π.
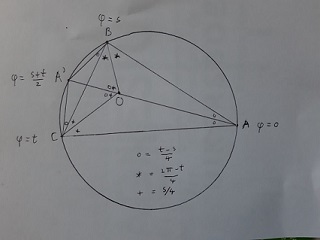
74 geometry (february 1897)
O is the center of the inscribed circle of triangle ABC. AO meets the circumcircle in A'. Find AO/A'O.
Solution:
We start from the circumcircle with parametrization (cos(φ),sin(φ), 0 ≤ φ ≤ 2π.
O is the intersection point of the angle bisectors, so we get the following picture:

We see A'O = A'C = A'B = 2 sin((t-s)/4) and AA' = 2 sin((t+s)/4).
So AO/A'O = sin((t+s)/4)/sin((t-s)/4) - 1, depending on s and t.
90 average and probability (january 1900)
During a heavy rain storm a circular pond is formed in a circular field. If a man undertakes to cross the field in the dark, what is the chance that he will walk into the pond?
Criticism and partial solution:
Give coordinates in such a way that the circular field has center (0,0) and radius 1, and the man starts from (-1,0).
We take for granted the man walks along (-1,0) + λ(cos(θ),sin(θ)), λ > 0, where every direction θ between -π/2 and π/2 is equally probable.
Now the circular pond may have equation (x - ρcos(α))2 + (y - ρsin(α))2 = R2 for any α ∈ [0,2π) and any ρ < 1 and any R between 0
and 1-ρ.
We assume every α is equally probable, so the probability of α lying in an infinitesimal range δα is δα/(2π).
We also assume that the distance of the center of the pond from the center of the field is lying between ρ and ρ + δρ
for some positive infinitesimal δρ with a chance equal to 2πρ δρ/π.
But we can't make any reasonable assumption about the radius R of the pond, given ρ, without further info.
We have to know the probability density function fρ(R) with ∫01-ρ fρ(R) δR = 1.
We now calculate the probability of the man walking into the pond if α, ρ and R are given.
This probability is P(α,ρ,R) = (θ2 - θ1)/π, with θi corresponding to the pair of walks that are tangent to the pond.
I find cos(2θi ) = (BC ± A √(A2 + B2 - C2))/(A2 + B2), where
A = ρsin(α) + ρ2sin(α)cos(α),
B = 1/2 + ρcos(α) + ρ2cos(2α)/2,
C = ρ2/2 + ρcos(α) + 1/2 - R2.
The chance asked for is ∫02π ∫01 ∫01-ρ P(α,ρ,R) fρ(R) 2πρ δR δρ δα/(2π2).
171 number theory and diophantine equations (march 1910)
Solve completely: 2x2 - 1 = y, 2y2 - 1 = z, 2z2 - 1 = w, 2w2 - 1 = x.
Solution:
We find:
y = 2x2 - 1,
z = 8x4 - 8x2 + 1,
w = 128x8 - 256x6 + 160x4 - 32x2 + 1,
x - 1 = (215x16 - 217x14) + (13*214x12 - 11*214x10) +
(165*29x8 - 21*210x6) + (21*27x4 - 27x2).
Now we see: if |x| ≤ 1 then x=1 and if |x| ≥ 2 there is no solution.
So the only solution is x=y=z=w=1.
208 average and probability (december 1911)
Find the chance that the distance between two points in a square shall not exceed a side of the square.
Numerical solution:
If I take two random points an indeterminate number of times, the outcome seems to fluctuate a bit below 0.975.
The corresponding pascal program is the following:
program chance;
var a,b,x1,x2,y1,y2:real;
begin
a:=0; b:=0;
while true do
begin
x1:=random; x2:=random;
y1:=random; y2:=random;
if (((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)) <= 1) then a:=a+1 else b:=b+1;
writeln(a/(a+b):13:11)
end
end.
If I take 100*100*100*100 lattice points, the outcome is 0.9750...
The corresponding pascal program is the following:
program integraal;
var j,k,m,n:integer; p,q:real;
begin
p:=0; q:=100*100*100*100;
for j:=0 to 99 do for k:=0 to 99 do
for m:=0 to 99 do for n:=0 to 99 do
if (((j-k)*(j-k)+(m-n)*(m-n)) <= 10000) then p:=p+1;
writeln(p/q:10:8); readln
end.
But if I take 200 and then 300 and then 400 and then 500 instead of 100, it becomes clear the right answer is 0.9749 in four decimals and the fifth decimal is probably 3.
295 calculus (june 1910)
A hawk can fly v feet/second, a hare can run w feet/second. The hawk, when A feet vertically above the hare, gives chase and catches the hare when the hare has run B feet.
Find the length of the curve of pursuit.
Solution and criticism:
We suppose both go always at maximal speed.
If the hare chooses a path with parametrization x(t), and he runs his B feet during a time of T seconds, we have B = ∫0T ||x'(t)|| dt = Tw.
If the curve of pursuit of the hawk has parametrization y(t), and he flies L feet during the T seconds, we have L = ∫0T ||y'(t)|| dt = Tv = Bv/w.
But, in fact, B can't be known beforehand, and neither can x(t).
If we knew x(t), we could find y(t), and hence T and B, by solving y' = w(x-y)/||x-y|| and y(T) = (..,..,0)
with x(0)=(0,0,0) and y(0)=(0,0,A).
362 number theory (october 1911)
Show that the number of solutions in non-negative integers of the equation x + 2y + 3z = 6n is equal to 3n2 + 3n + 1.
Solution:
We proceed with induction.
The assertion is clearly true for n=0.
Suppose the assertion is true for n=m, i.e. suppose the number of solutions in non-negative integers of the equation x + 2y + 3z = 6m is 3m2 + 3m + 1.
Then any of these solutions, say (x,y,z) = (a,b,c), gives a solution (a+1,b+1,c+1) of x + 2y + 3z = 6(m+1).
On the other hand, each solution (A,B,C) of x + 2y + 3z = 6(m+1) comes from a solution (A-1,B-1,C-1) of x + 2y + 3z = 6m, unless ABC = 0.
Furthermore, the number of solutions of x + 2y = 6m+6 is 3m + 4, the number of solutions of x + 3y = 6m+6 is 2m + 3, and the number of solutions of 2y + 3z = 6m+6 is m + 2,
and among these solutions with ABC = 0, three of them are counted twice.
So the total number of solutions of x + 2y + 3z = 6m+6 is (3m2 + 3m + 1) + (3m + 4) + (2m + 3) + (m + 2) - 3 = 3(m+1)2 + 3(m+1) + 1.
382 geometry (february 1911)
Between the side of a given rhombus and its adjacent side produced, to insert a straight line of a given length and directed to the opposite corner. (Euclidean constructions are
particularly desired.)
Numerical solution:
Let the given length be L, so L is a given positive real.
Take coordinates so that the vertices of the rhombus are A(-1,0), B(0,t), C(1,0) and D(0,-t) for some given positive real t.
Consider the side AD and take for positive real p a variable point P(-1-p,-pt) on BA produced. We have to find p so that the line through P and C intersects AD in Q with PQ=L.
We find p4(1+t2) + 4p3 + 4p2 = L2(p+1)2.
Now if we don't want to use the formulas of Cardano cs, we may find a rational approximation for p that's as accurate as we want.
389 geometry (april 1911)
On the same side of a given base, triangles are erected such that the bisectors of their vertex angles all pass through a given point. Find the locus of the vertices.
Solution:
Let the given base be AB with A(-1,0) and B(1,0). Let the given point be P(a,b) for some negative b.
Let the vertex be V(s,t) for some positive t.
For the vertex angle φ we find cos(φ) = (s2+t2-1)/(√((s+1)2+t2)√((s-1)2+t2)).
Now we demand that the angle AVP be φ/2, so cos(φ/2) = (s2+t2+s-as-bt-a)/(√((s+1)2+t2)√((s-a)2+(t-b)2)).
The required locus is found by cos(φ) = 2cos2(φ/2) - 1, which yields
(s2+t2-1)/(√((s+1)2+t2)√((s-1)2+t2)) = 2((s2+t2+s-as-bt-a)/(√((s+1)2+t2)√((s-a)2+(t-b)2)))2 - 1.
We can plot this for any given a,b, using https://www.desmos.com/calculator.
399 geometry (january 1912)
A race track is to be composed of two tangents and the arc of a circle which is concave towards the point of intersection of the two tangents, each tangent and the arc of the circle being 1 mile.
What is the radius of the circle?
Solution:
If the tangents touch the circle in r(-cos(t),sint(t)) and r(cos(t),sin(t)), we find r = tan(t) = 1/(π-2t).
Hence t is about 0.405235 radians and r is about 0.429 mile.
I don't think a much more exact answer is possible.
2922 A telephone engineer desires the general solution of the following differential equation: xy" + y' = a/√y.
Partial solution:
Let u = √y, so u > 0 and xu(u')2 + xu2u" + u2u' - a/2 = 0 for all x.
We substitute u = a0 + a1x + a2x2 + a3x3 + ...
and set all coefficients of xk (k = 0,1,2,...) equal to 0. Then we get:
a02a1 - a/2 = 0,
3a0a12 + 4a02a2 = 0,
2a13 + 14a0a1a2 + 9a02a3 = 0,
11a12a2 + 26a0a1a3 +
12a0a22 + 16a02a4 = 0,
etc.
Let a0 = c > 0. Then a1 = a/(2c2), a2 = -3a2/(16c5),
a3 = 17a3/(144c8), a4 = -415a4/(288c11), etc.
Continuing this way, we can calculate as many ak as we want.
Now for each a we can choose c so that the power series has a positive radius R of convergence, and for given x with
|x| < R and positive integer n we can find an upper and lower bound for the sum of the terms
akxk with k > n.
2937 A straight uniform stone wall AB is to be rebuilt in another position CD, the intersection of AB and CD being interior to CD but not to AB. How should the material be moved for the average horizontal distance through which it is carried to be as short as possible? If CD passes through B, show that the lower limit to the average distance may be expressed by means of logarithms and algebraic functions.
Solution:
The given things may be reformulated as follows:
A(0,0), B(1,0), C(p,q), D(p-cos(t),q-sin(t)) with 0 < q < sin(t) ≤ p sin(t) - q cos(t).
Furthermore, we assume A is not closer to D than to C, which amounts to p cos(t) - q sin(t) ≤ 1/2.
Then the motion is described by the affine transformation H(x,y) = (-x cos(t) + y sin(t) + p, -x sin(t) -y cos(t) + q), which is the composition of a rotation and a translation with H(A) = C and H(B) = D.
Now CD passes through B iff sin(t) = p sin(t) - q cos(t), or p = 1 + q cotan(t).
The lower limit to the average distance asked for is found by integrating the distances from (s,0) to W(s,0), so we get
∫ 01 √ ((p - s cos(t) -s)2 + (q - s sin(t))2) ds =
∫ 01 √ (U + V(s - W)2) ds.
It's well known this integral is a composition of logarithms and algebraic functions.
2953 An algebraic equation being known to have exactly n real roots, all simple, is it possible to find an equation of degree n-1 whose roots separate those of the given equation and whose coefficients are rational functions of the coefficients of the given equation?
Solution:
Suppose the given equation is
xn - sn-1xn-1 + ... + (-1)ns0 =
(x - a1) (x - a2) ... (x - an) = 0,
so the coefficients si are the
elementary symmetric expressions in the roots a1 < a2 < ... < an.
Suppose the equation we seek is
xn-1 - tn-2xn-2 + ... + (-1)n-1t0 =
(x - b1) (x - b2) ... (x - bn-1) = 0,
so the coefficients ti are the
elementary symmetric expressions in the roots b1 < b2 < ... < bn-1.
Let bi :=λiai + (1-λi)ai+1 for
rational numbers λi in the interval (0,1).
The question is whether we can choose these rationals λi so that the coefficients ti are rational
functions of the coefficients si and hence symmetric expressions in a1, ... , an.
For instance, if we choose λi = 1/2, then
tn-2 = b1 + b2 + ... + bn-1
= a1/2 + a2 + ... + an-1 + an/2, which is not symmetric.
In fact, tn-2 is only symmetric if b1 + b2 + ... + bn-1 =
λ1(a1 + a2 + ... + an-1 + an), so if
λ1 = 1 - λi + λi+1 = 1 - λn-1 for i=1,2,..n-2.
It follows that λi = 1 - i/n.
But then t0 = b1b2 ... bn-1 = ((1 - 1/n)a1 + (1/n)a2)
((1 - 2/n)a2 + (2/n)a3) ... ((1-(n-1)/n)an-1 + (n-1)/n)an),
which is not symmetric.
So the answer is negative.
2958 Over a frictionless pulley a weightless cord sustains at one end a mass M, while the other end is wound on an axle of a wheel of mass M and moment of inertia N.
At the zero of time the wheel revolves with angular velocity ω and tends to wind up the cord.
Describe the motion, neglecting friction.
Solution:
For the angular velocity at time t we have ω(t) = dφ(t)/dt = dr(t)/dt, where the angle φ(t) and the loose end of length r(t) of the cord satisfy
φ(t) - φ(0) = r(t) - r(0) (mod 2π).
Since the moment of inertia comes from gravity, we have N = Mg = (dω(t)/dt) M r(t)2 = (d2r(t)/dt2 M r(t)2 as long as ω(t) ≤ 0, so
r(t)2 (d2r(t)/dt2 = g, with r(0) = r0 and r'(0) = ω.
To solve this differential equation we try a power series r(t) = r0 + ωt + r2t2 + r3t3 + r4t4 + ...
We find r2 = g/(2r02), r3 = -gω/(3r03), r4 =
(g2-3gr0ω2)/(12r05), etc.
2959 Solve the functional equation g(x)2 = -2x + g(x2).
Solution:
If g is a real solution then 1 and -1 are not in its domain, because there's no real c with c2 = -2 + c.
Furthermore, g(0) must be either 0 or 1.
Whenever A is a real that doesn't belong to {0,1,-1}, and c is any real, there exists infinitely many solutions with g(A) = c and g(A2) = c2 + 2A.
For example, if g(1/2) = c then g(1/4) = c2 + 1 and g(1/16) = (c2 + 1)2 + 1/2, etc.
This solution may be combined with, for instance, g(1/3) = c' and g(1/9) = c'2 + 2/3, etc, for any real c'. However, g(-1/2) must be equal to ± g(1/2).
If the domain of g consists of all reals not equal to 1 or -1, g can't be continuous, because the sequence g(1/2), g(1/4), (g(1/16) ... can't tend to g(0).
2965 If a quadrilateral inscribed in a square has the diagonals a and b, and the area A, show that the area of the square is (a2b2-4A2)/(a2+b2-4A).
Sketch of a solution:
Give coordinates so that the square has vertices (0,0), (r,0), (r,r) and (0,r).
Let the quadrilateral have vertices (0,s) and (t,0).
Then the other two vertices must be ((s(r-s)/t,r) and (r,t(r-t)/s) and we must have r = (t3+t2s+ts2+s3)/(t2+s2).
So for the diagonals we find a = √(t4+s4-2s3r-2t2sr+2s2t2+s2r2+r2t2)/t
and b = √(t4+s4-2t3r-2s2tr+2s2t2+s2r2+r2t2)/s,
and for the area we find A = √(s2+t2)√(r2s2+t2s2-2rs2t+t2r2+t4-2t3r)/s.
Now we still have to work out that r2 equals (a2b2-4A2)/(a2+b2-4A), but perhaps 4A is an error and should be should be 4A2.
We leave this to someone more diligent.
2967 A plane revolves about one of two non-coplanar lines as an axis. Find the locus, in the plane, of the intersection of the plane and the other line.
Solution:
By the principle of relativity, we may keep the plane fixed and let the rest of space merrily go around.
Let the plane have parametrization (x,y,0) and the axis λ(sin(α),0,cos(α)) and the other line (a,b,0) + μ(p,q,1).
During the revolution of the axis about the normal of the plane, the angle between the direction vector of the axis and the normal vector (0,0,1) of the plane remains α,
so after φ degrees of revolution the revolved axis has parametrization λ(sin(α)cos(φ),sin(φ),cos(α)).
Then the other line in its revolved position has parametrization ((a+μp)cos(φ),(b+μq)sin(φ),μ) and its point of intersection with the plane is (a cos(φ),b sin(φ),0).
So the locus of this point of intersection is an ellipse.
2970 For which positive integers k,m,n is k times cosm(2π/n) a quadratic integer?
Partial solution:
For n=1, any m, and k a quadratic integer;
for n=2, even m, and k a quadratic integer;
for n=3, even m, and k equal to (2m times a quadratic integer).
for n=4, and arbitrary m and k;
for n=6, any m, and k equal to (2m times a quadratic integer);
for n=8, even m, and k equal to (2m/2 times a quadratic integer).
For each n, we can find (infinitely many) k iff cosm(2π/n) is a (positive) rational number u/v: take k := (v times (any j such that j times u is a quadratic integer)).
I guess the only other possible n is n=12: then for even m we have u/v = (3/4)m/2.
2971 Prove in an analytical way that the two tangents drawn to an ellipse from any external point subtend equal angles at a focus.
Sketch of a solution:
Give coordinates such that the ellipse E has equation x2/a2 + y2/b2 = 1 (a ≥ b) with focuses F(±c,0) where c = √(a2-b2).
Let S and T be any two points on E, say S(a cos(s), b sin(s)), T(a cos(t), b sin(t)) for s,t ∈ [0,2π).
The tangents at S and T intersect at P(a(sin(s)-sin(t))/sin(s-t),b(cos(t)-cos(s))/sin(s-t)).
We have to prove that the angles ∠PFS and ∠PFT are equal, which could be done straightforwardly by using the cosine rule.
2972 We learn about the following proposed "approximate compass and straightedge tripartitions of 'any' angle":
(a) Let β be the angle ABC, where AB=CB. Find P within this angle so that the line through P and C is parallel to the line through A and B and PC=AC.
Then the angle φ := ABP is approximately equal to β/3.
(b) In the situation of (a), find Q on CP so that CQ=2*AB and find R between P and Q so that PR:RQ = 5:4.
Then the angle φ := ABR is approximately equal to β/3.
Study these approximations and discuss how good they are.
(c) Propose better approximations yourself.
Solution:
(a) After applying the cosine rule in triangles ABC, ACP, BCP and ABP, respectively, and using some goniometrical formulas, we find :
cos(φ) = (1 + 4(4t2-1)3(1-t2)√(1-t2) - 2(4t2-1)2(1-t2) + 2(4t2-1)√(1-t2)(32t6-48t4+18t2-1)) / √(1 + 4(4t2-1)2(1-t2) + 4(4t2-1)√(1-t2)(32t6-48t4+18t2-1)) , with t = cos(β/6).
Now we calculate φ for each integer β in the range from 1 to 179 degrees with the help of a device we call 'computer'.
We see the estimate φ is too large for small β and too small for large β.
It turns out φ is only between 80 and 120 percent of β/3 for β between 87 and 128 degrees. And β/3 = φ only for β=108 degrees.
(b) In a way analogous to (a), we find:
cos(φ) = (19 + 8u - 18u2) / √(361 + 304u -296u2 -288u3), with u = sin(β/2).
(After my experience with (a), I don't think it's useful to express u in t = cos(β/6).)
Of course, since φ is smaller than in (a), we expect this estimate to be better than in (a) for small angles, and worse for large angles.
It turns out φ is between 80 and 120 percent of β/3 for β between 46 and 121 degrees. And the best fit is φ=1.002*β/3 for β=90 degrees.
So this one is a reasonable estimate for a much larger range of β.
(c) In order to find better approximations, we may construct a line segment of length z:= p*AC + q*AB for rational p and q.
Let T be the point within angle ABC so that CT is parallel to AB and T is at distance z from C.
Let φ be the angle ABT.
Again, by using the cosine rule four times, we find:
cos(φ) = (1+2pu +q-2u2) / √(1+(2pu+q)(2pu+q+2-4u2)), with u = sin(β/2).
Now for all p and q such that 90p and 90q are integers belonging to {0,1,..,360}, we calculate the number of integer β between 0 and 180 degrees such that
φ is between 80 and 120 percent of β/3.
We find this number is maximal for p=0 and q=135/90=3/2, and then the range of β for which the approximation is reasonable is {1,2,3...,147}.
When proposers of problems wouldn't lead us astray, we would simply divide AC in three equal parts:
Take S on AC so that AS=AC/3. Let φ:= angle ABS.
Then cos(φ) = (3-2u2)/(sqrt(9-8u2), and φ is between 80 and 120 percent of β/3 for all β ≤ 111 degrees
(and, in fact, φ is always smaller than β/3).
So this one is better than the constructions proposed in (a) and (b), if we only look at the range of β for which the estimate is reasonable.
If we take S on AC so that AS=a*AC/3 for some rational a between 1 and 1.3 for which 100a is integer, we get cos(φ) = (3-2*a*u2)/(sqrt(9-12a*u2+4*a2u2).
It turns out the range of reasonable β is maximal for a=1.19. Then this range is {1,2,..,146}.
But I think B and the best points S and T must be collinear, which holds for p=0, q=3/2, a=1.2 (with AS = 2AC/5).
The difference beween 1.19 and 1.2 clearly stems from rounding errors.
We conclude the best (and easiest to perform) approximate straightedge and compass angle tripartition that we found is as follows:
1) Construct through C a line parallel to AB.
2) Find on this line the point T within angle ABC so that TC = 3AB/2.
3) The angle φ := ABT is a reasonable (between 80 and 120 percent) estimate of β/3 if β is at most 147 degrees.
(We also find φ is between 90 and 110 percent of β/3 for β between 99 and 139 degrees, and the estimate is best for β=124 degrees.)
Further solutions: click here .