This problem is dedicated to my maths teacher (1967-1969) at the gymnasium in Zenderen (Overijssel), mr G.A.Jansen, and to my teachers in Nijmegen and Eindhoven, especially the professors Levelt and van Lint.

Four mutineers arrive on a circular island with a radius of one kilometer. Three of them are friends, called Alonzo, Bernd and Christian; the fourth is a dangerous fool, called Pierre.
The friends want to settle at the beach and use the triangle between them to grow potatoes. The area of this potato field must be one square kilometer. But they want Pierre to settle as far away as possible. Or is it perhaps better to have him settle as near as possible, maybe even in the potato field?
To build a model on a small scale, we change the kilometer into a meter.

Suppose you have a circle with a radius of one meter.
1) Find the positions of three points A,B,C on the circle and a point P inside or on the circle such that the area of triangle ABC is equal to one square meter, and such that, if you add the distances from P to A, from P to B and from P to C, the outcome is as great as possible; how many meters is this maximal distance sum PA+PB+PC?
2) As 1), but now PA+PB+PC has to be as small as possible (so we seek the minimal distance sum) .

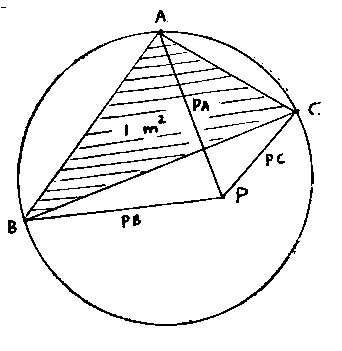
Always choose A like in the picture, so A is the highest point on the circle. Choose B somewhere to the left on the circle. Of course, P can lie inside the triangle or on the circle. But to solve the problem you have to consider all possible triangles ABC that match the restrictions.

Show clearly how you seek the answers, how you find them, and how you verify them.
You may use the computer or the measuring rod, if you want, but exact answers are better than approaching ones.
There is a nice little prize in each of three categories:
category A- using only primary school maths;
category B- using secondary school maths;
category C- using all possible higher maths.

The best solution in each category will be published in this website, together with my own solutions, with the name of the solver.

You may send your solutions by e-mail (but then without attachments), or by traditional mail. I will acknowledge the receipt as soon as possible. Send your solutions with complete name and address data to
H.Reuvers, Brusselsestraat 92, 6211 PH Maastricht Nederland
(e-mail info@petericepudding.com) .
Applications close on the 10-th of Januari. Thereafter it may last one or two weeks before the results will be published.