The lonely runner
Problem:
Some athletes start together at the same starting point for a running contest over a circular track. They keep running clockwise around forever at fixed distinct speeds. At some instant of time each
runner may be at equal distance d from the one who runs before him and the one behind him, so that the positions of the runners are evenly distributed over the track. But is there for each of them an
instant of time when he is at distance at least d from any other runner?
The conjecture that JM Wills made in 1967 says there is such an instant of time. The problem is how to prove this. This problem has been solved for up to seven runners, but the general problem remains
unsolved.
In mathematical terms, we may formulate the problem for k+1 runners as follows:
Given a positive integer k, and k integers d1 , d2 , ... , dk without common prime divisor. Prove there is a positive real t such that for all i∈{1,2,..,k} the
product tdi is at distance at least 1/(k+1) from the nearest integer.
First approach:
Denote the distance of any real number x from the nearest integer by ||x||.
We may use the following Pascal program to search for an approximation of the minimal t if k is at most 100 and the k given integers are within standard pascal range:
program runner;
var i,j,k:integer; t:real; d:array[1..100] of integer; noggoed:boolean;
function norm(x:real):real;
begin
norm:=abs(x-round(x))
end;
begin
writeln('k?'); readln(k);
writeln('Geef ',k:3,' positieve integers');
for j:=1 to k do begin writeln('d[',j:3,']?'); readln(d[j]) end;
t:=0;
repeat
t:=t+0.00001;
noggoed:=true; i:=0;
while ((i < k) and noggoed) do
begin i:=i+1; if norm(t*d[i]) < (1/(k+1)) then noggoed:=false end;
if noggoed then
begin
writeln(t:13:5); for j:=1 to k do writeln(norm(t*d[j]):13:10);
writeln; readln
end
until noggoed
end.
The 3n+1 conjecture
Problem:
Take an arbitrary positive integer n. If n is even, change it into n/2. If n is odd, change it into 3n+1. Show that if we repeat this procedure, we get 1 in the end.
First approach:
If n is even, then the probability that n/2 is even is 1/2 again. We count n → n/2 as one step.
If n is odd, then 3n+1 is even and the probability that (3n+1)/2 is even is 1/2 again.
We count n → 3n+1 → (3n+1)/2 as one step.
After k steps we expect to have less than (n+1)*(√3/2)k, which tends to 0 if k → ∞.
So we should get 1 in the end.
The square in the loop
Problem:
Prove that in any loop that doesn't intersect itself there exists an inscribed square.
First approach:
With a pascal program we may systematically search for four points on the loop that are the vertices of a square.
As an example, I did this with the raindrop (t3-3t,3t2), -√3 ≤ t ≤ √3,
and found (approximated values of t, x, y, resp):
A -1.28 -1.74 4.93
B -0.69 -1.75 1.44
C 0.69 1.75 1.44
D 1.28 1.74 4.93
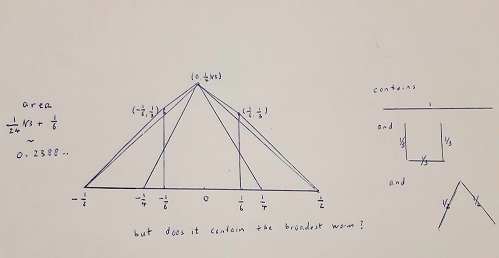
Worms
Problem:
Find the minimal area that can cover any curve of unit length.
First approach:

A generalized Fermat problem
Problem:
For which 6-tuples x,y,z,m,n,k of positive integers holds xm + yn = zk?
First approach:
The set of all 6-tuples of positive integers is countable, so we may see whether the equation holds or not for every such 6-tuple in turn, in the order of an enumeration of all these 6-tuples.
Idoneal numbers
Problem:
Which positive integers are not of the form ab + ac + bc for distinct positive integers a,b,c?
First approach:
We easily find all 65 known idoneal numbers among the pascal integers with the help of a pascal program. The largest of these is 1848. But perhaps there exists an idoneal number greater than 32767.
The Kolakovski sequence
Problem:
Construct the unique sequence of 1's and 2's that begins with 1 and is equal to the sequence of its block lengths.
Is there a formula for the n-th bit of the sequence?
First approach:
We get 122112122122112112212... (with every 1 in the sequence we get one more 1 or 2 at the end of the sequence, and with every 2 in the sequence we get two more 1's or two more 2's at the end of the sequence).
Minimal sum on a sphere
Problem:
Given a positive integer n > 1, for which n points xk , 1≤k≤n, on a sphere with radius 1/2, is the sum Σ 1 ≤ i < j ≤ n log(1 / ||xi-xj||) minimal?
First approach:
I wrote and ran a pascal program to generate n points at random on the sphere many times and write down the sum and the coordinates of the points whenever the sum is less than before.
For example, for n=10 we get the following output:
15.79284
+0.40634 +0.06197 +0.28469
-0.23267 -0.44180 -0.02608
-0.01323 +0.00889 -0.49975
-0.18505 -0.07195 +0.45889
+0.22679 -0.40541 +0.18494
-0.22299 +0.37512 -0.24405
+0.36773 -0.21750 -0.25974
-0.20963 +0.36895 +0.26445
-0.46054 -0.08683 -0.17424
+0.25284 +0.42780 -0.05529
The outputs indicate that for small n the minimal sums are approximately equal to n2/4 - n + 1.
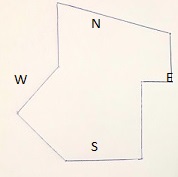
Lost in the forest
Problem:
A convict is dropped somewhere in a forest by a helicopter. He is equipped with a compass and a laptop that provides a map of the edge of the forest and a pascal compiler. Which path should he follow to get to the edge and escape from the forest?
Partial numerical solution:
I take it the convict decides to choose a fixed direction and head that way in a straight line until he reaches the edge.
To find the best direction among 360 directions with the help of a pascal program, he may make the edge input of the
program. This edge encloses a finite but large number of forest points.
Then, for each of the 360 directions, he can find among these forest points a worst point
for which the distance to the edge, when heading from that point in that direction, is maximal.
Finally, he will choose a direction for which this worst distance is minimal.
For example, the map and the program might be the following:
program forest;
var d,k,m,n,s,t,max,min:integer; bos:array[-500..500,-500..500] of boolean;
procedure walk(s,t,k:integer;var d:integer);
const pi = 3.14159265359;
var x,y:real;
begin
x:=s; y:=t; d:=0;
while bos[round(x),round(y)] do
begin
d:=d+1; x:=x+cos(pi*k/180); y:=y+sin(pi*k/180)
end
end{walk};
begin
for m:=-500 to 500 do for n:=-500 to 500 do bos[m,n]:=true;
for m:=-500 to 500 do begin bos[m,-500]:=false; bos[m,500]:=false end;
for n:=-500 to 500 do begin bos[-500,n]:=false; bos[500,n]:=false end;
for m:=-500 to -200 do for n:=-500 to -700-m do bos[m,n]:=false;
for m:=-500 to -200 do for n:=m+300 to 500 do bos[m,n]:=false;
for m:=-200 to 500 do for n:= ((2900-3*m) div 7) to 500 do bos[m,n]:=false;
for m:=300 to 500 do for n:=-500 to 0 do bos[m,n]:=false;
min:=1000;
for k:=0 to 359 do
begin
max:=0;
for s:=-500 to 500 do for t:=-500 to 500 do
if bos[s,t] then
begin
walk(s,t,k,d);
if d > max then max:=d
end;
if max < min then begin min:=max; writeln(min:5,k:5) end
end;
readln
end.
The output is:
799 0
793 129
779 130
778 132
777 133
776 135
So this convict should head north-west.
The inverse polynomial question
Problem:
Suppose ui(x1,...,xn) are polynomials (i=1,..,n) and the jacobian
det(δui /δxj) is constant and not 0.
Prove that
xi(u1,...,un) are polynomials (i=1,..,n).
First approach:
As an example we take (u1,u2) = (x12 + 2x1x2 +
x22 + x1, x1 + x2) with constant jacobian 1.
The inverse is (x1,x2) = (u1 - u22,
u22 + u2 - u1).