EO: nadere aanwijzingen:

1.
a) ψ is het product van de elementaire perspectiviteiten van l naar A naar K naar B naar l, de restrictie tot l van de polariteit, en de elementaire perspectiviteit van L naar l.
b) Maak een tekening, en laat zien dat C, D en O: λ(0,0,1) in zichzelf overgaan. Omdat ψ drie dekpunten heeft, is ψ de identiteit.
c) (Eenvoudig. Voor de constructie van de poollijn, zie §22.)
d) Ga na dat C en D altijd dekpunten zijn.
e) Als X = AE . l, dan S_X = E. Stel nu Y = BS_X . l. Construeer het andere snijpunt Z van AY met K mbv Pascal. Dan is y de niet door Y gaande diagonaal van ABEZ, en ψ(X) = y . l.
f) (Als in de uitwerking van O102, fragment Kaper-Westerman; neem voor J een cirkel.)
g) X : λ(0,√2-1,1) met ψ(X) = λ(0,(1/2)√2,1). Eis nu van een drie bij drie matrix dat hij (0,√2-1,1) overvoert in een scalair veelvoud van (0,(1/2)√2,1), en (0,1,1) en (0,-1,1) in scalaire veelvouden van zichzelf.

2. π is het product van de restrictie tot l van de polariteit mbt K en de elementaire perspectiviteit van L naar m.
Is p de Pappuslijn, dan π(l . m) = p . m en π(l . p) = l . m.
Dus LM . m = p . m en LP . m = l . m.
Dus LM gaat door p . m en (omdat l . m op LP ligt) door l . p.
Dus p = LM.

3. Zijn A, B, C, D, E de gegeven punten dan kan men voor φ nemen de lijnenwaaierprojectiviteit van A naar B die aan AC toevoegt BC, aan AD toevoegt BD, aan AE toevoegt BE. De te construeren snijpunten zijn dekpunten van de op l geïnduceerde projectiviteit. Deze construeert men mbv een hulpcirkel als in het fragment Kaper-Westerman in de uitwerking van O102.

4. Laten A, B, C, D de gegeven eigenlijke punten zijn, en O het gegeven oneigenlijke punt.
Construeer de loodlijn op AO door A. Zij S het andere snijpunt van deze loodlijn met de kegelsnede. Construeer S door Pascal toe te passen op zeshoek ABC-DOS.
Construeer de middelloodlijn van [AS]. Deze lijn gaat door O en de te construeren top T. Construeer T door Pascal toe te passen op zeshoek AOD-CBT.

5. Dit gaat met de methode der valse posities. (Zie de uitwerking van O102.) Dus:
Start met een willekeurig punt X op l. Verbind dit punt met A en snijd de verbindingslijn met de oneigenlijke lijn. Verbind dit oneigenlijk punt met C en snijd de verbindingslijn met m. Verbind dit snijpunt met D en snijd de verbindingslijn met de oneigenlijke lijn. Verbind dit oneigenlijk punt met B en snijd de verbindingslijn met l. Noem het snijpunt X '.
De toevoeging X → X ' is een projectiviteit van l op zichzelf. Construeer nog bij twee andere punten X het beeldpunt X '.
Construeer nu de dekpunten van deze projectiviteit, zoals in het eerste fragment van de uitwerking van O102. (Gebruik voor J een cirkel, dan blijft het een constructie met passer en lineaal.) Het zijn er nul, een of twee.
Als je begint met een dekpunt X, dan levert de constructie een oplossing van het probleem (en het punt Y op m).

6.

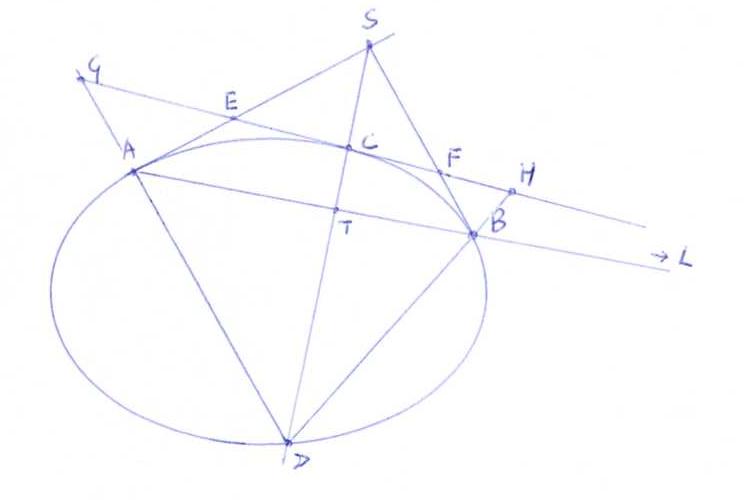
L ∈ s ⇒ S ∈ l
L ∈ c ⇒ C ∈ l
Dus l = SC (en LD is raaklijn in D aan K).
Is T := AB . SC, dan scheidt {L, T} dus harmonisch met {A, B}.
Door projecteren vanuit S zien we dan dat {L, C} harmonisch scheidt met {E, F}.
Door projecteren vanuit D zien we dat {L, C} harmonisch scheidt met {G, H}.

Zij J de kegelsnede door A, B, D, E en F.
Vanwege de eerste twee bovengenoemde harmonische liggingen is SC eveneens poollijn van L tov J. Omdat D op deze poollijn ligt, moet L op de raaklijn in D aan J liggen.
Dus LD raakt in D zowel aan K als aan J.

7. Een kegelsnede, want φ is een projectiviteit en genereert een projectiviteit van A naar B. De kegelsnede is in concrete gevallen eenvoudig punt voor punt construeerbaar.

8. De poollijn van de top is de raaklijn x₂ = 0 met projectieve coördinaten λ(0,1,0). De poollijn van het oneigenlijk punt op de as is de raaklijn x₃ = 0 met projectieve coördinaten λ(0,0,1). Het snijpunt van deze twee raaklijnen is het oneigenlijk punt op x₂ = 0, dus λ(1,0,0). Dat is dus de pool van de as van de parabool.

9. K wordt voortgebracht door φ : A → B met φ(AS) = BS, φ(AT) = BT, φ(AC) = BC.
K ' wordt voortgebracht door ψ : A → B met ψ(AU) = BU, φ(AV) = BV, ψ(AC) = BC.
Construeer ψ^-1(BS) en ψ^-1(BT) met de stelling van Steiner.
Aldus vinden we van θ := ψ^-1φ : A → A de beelden van AS, AT en AC (laatstgenoemde is invariant). Vinden we nog een tweede invariante lijn x, dan is φ(x) = ψ(x), dus x . φ(x) = x . ψ(x), dus dat levert dan een vierde snijpunt van K en K '.
Zo'n tweede invariante lijn construeren we als volgt:
θ induceert op een willekeurig gekozen lijn l die niet door A gaat een projectiviteit ω := ε^-1θε waarbij ε elementaire perspectiviteit van verbinding van l naar A. Ook van ω kennen we dus een dekpunt en twee andere paren van punt en beeldpunt. In het algemeen is er nog één tweede dekpunt (anders zijn K en K ' rakend of samenvallend). Construeer dit tweede dekpunt als in O52.

10. Pas Brianchon toe op d b α - a δ c. Dan blijkt dat α . δ ligt op de vaste lijn ((D-(a . b)) . (A-(c . d))) - (b . c).

11. Past men Pascal toe op A C D₁ - D B A₁ en op B₁ C D₁ - C₁ B A₁, dan blijkt dat CA₁ . BD₁ op OL en OM ligt.

12.
a) Pas Brianchon toe op a b c - c a b .
b) Past men Brianchon toe op a b c - b a l, dan blijkt dat de lijnen A₁B₁ allemaal gaan door ((b . l) - (a . c)) . ((a . l) - (b . c)) .
c) AA₁ → BB₁ is een projectiviteit van A naar B (product van de elementaire perspectiviteit van A naar BC, de perspectiviteit van onderdeel b) van BC naar AC en de elementaire perspectiviteit van AC naar B).
Deze projectiviteit φ brengt de in de opgave genoemde kegelsnede voort.
Zij gaat door A en B en, omdat φ(AC) = BC, ook door C.