§ 6: uitwerkingen

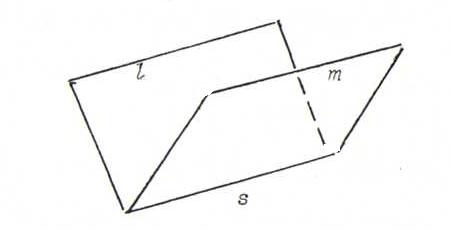
O22 Zijn l en m lijnen in P², die corresponderen met vlakken α en β door 0 in ℜ³, dan heten l en m evenwijdig indien ze elkaar snijden in een oneigenlijk punt (dus indien de snijlijn s van α en β in γ:{x₃=0} ligt).

Neemt men een projectieve transformatie φ, afkomstig van de reguliere lineaire transformatie A, dan zijn φ(l) en φ(m) evenwijdig precies dan als A(s)⊂γ, dus precies dan als A tevens affien is.
Immers A(α)∩A(β) = A(α∩β) = A(s), en φ(l) en φ(m) zijn evenwijdig precies dan als A(α)∩A(β) in γ ligt.

O23 De hoek θ tussen twee lijnen l en m in x₃=1 blijft invariant onder de gelijkvormigheidstransformatie die ontstaat door eerst loodrecht te projecteren op x₃=0, dan in x₃=0 een ρ-voud van een draaiing of spiegeling toe te passen, en tenslotte te transleren over (a,b,1).
Evenzo blijft, als ρ=1, de afstand tussen twee punten in x₃=1 bewaard onder de samenstelling van deze drie afbeeldingen.

O24
Volledige vierhoek: P, A, G, C; parallellogram: A, G, C; vierkant en ruit: G, C.

Neem bijvoorbeeld de punten (0,0,1), (1,0,1), (0,1,1) en (1,1,1) in x₃=1, de hoekpunten van een vierkant.
Zij A de reguliere lineaire transformatie van ℜ³ met matrixrijen ((1,1,1),(0,0,1),(1,0,1)).
Dan, onder A, (0,0,1) → (1,1,1), dus φ(0,0,1)=(1,1,1); evenzo (1,0,1) → (2,1,2), dus φ(1,0,1)=(1, 1/2, 1); evenzo (0,1,1) → (2,1,1), dus φ(0,1,1)=(2,1,1); evenzo (1,1,1) → (3,1,2), dus φ(1,1,1)=(3/2, 1/2, 1).
Dus het beeld onder φ van dit vierkant is niet eens een parallellogram.
Blijkbaar zijn de begrippen vierkant, ruit en parallellogram niet projectief.

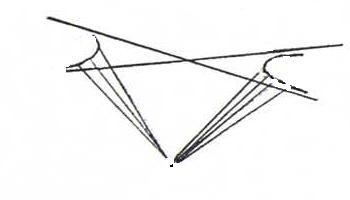
O25 Nee. Definieer een hyperbool als een kegelsnede die de oneigenlijke rechte L_∞ in twee punten snijdt. Voorbeeld: H met inhomogene vergelijking xy=1, homogene xy=z²; hierop liggen de oneigenlijke punten S:λ(1,0,0) en T:λ(0,1,0).

Zij nu φ een affiene transformatie, afkomstig van de reguliere lineaire transformatie A van ℜ³.
Dan {A(S), A(T)} = A(H∩L_∞) = A(H)∩A(L_∞) = A(H)∩L_∞, dus A(H) snijdt L_∞ weer in twee punten. Blijkbaar voert een affiene transformatie elke hyperbool in een hyperbool over.
Dus een hyperbool en een ellips kunnen nooit A-gelijk zijn.

O26 (A,B;C,L_∞) = AC/BC, dus:
i) (A,B;X,L_∞) kleiner dan 0;
ii) (A,B;C,L_∞) ∈ {4,-2};
iii) (A,B;C,L_∞) = -1.