§ 15:

O59 Stel dat A, B, C, D de vrijgelegen dekpunten zijn.
Omdat A en B dekpunt zijn, is de lijn AB invariant. Evenzo is CD invariant. Dus is het snijpunt S₁ van AB en CD dekpunt.
De lijnen AB en CD bevatten dan elk drie dekpunten, en zijn dus puntsgewijs invariant (FS §10). Zo is elk der lijnen van vierzijde ABCD puntsgewijs invariant.
Zij nu X een willekeurig punt in P². Kies een lijn door X die vierzijde ABCD in minstens drie punten snijdt. Dan bevat deze lijn drie dekpunten, en is dus puntsgewijs invariant. Dus is X dekpunt. Omdat dit voor elke X geldt, is de projectieve afbeelding de identiteit.

O60 Dat φ een bijectie θ induceert van de lijnenwaaier L naar de lijnenwaaier φ(L) volgt uit de definitie van een collineatie. Omdat φ een projectieve transformatie is, bewaart θ de dubbelverhouding. Volgens de tweede stelling van §10 is θ dus een projectiviteit.
Indien φ twee waaiers lijn voor lijn invariant laat, vindt men gemakkelijk vier vrijgelegen dekpunten, want het snijpunt van twee invariante lijnen is een dekpunt. Volgens O59 is φ dan de identiteit.

O61 Stel c = a + λ(b - a), met λ niet in {0,1}. Dan P(c) = P(a) + λ(P(b) - P(a)).
Dus zijn P(a), P(b), P(c) collineair en P(A)P(B) / P(A)P(C) = ||P(a) - P(b)|| / ||P(a) - P(c)|| = 1/|λ| = ||a - b|| / ||a - c|| = AB / AC.
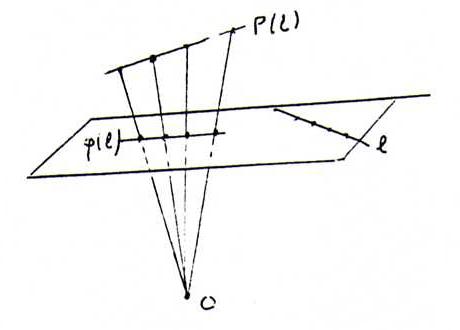
Zijn nu A, B, C, D vier punten op een lijn l in {x₃ = 1}, dan geldt:
(A, B; C, D) = (P(A), P(B); P(C), P(D)) = (φ(A), φ(B); φ(C), φ(D)) (projectie van P(l) op φ(l) vanuit O).