§ 10: uitwerkingen

O39 Duale fundamentele stelling; gegeven drie lijnen a, b, c door een punt L en drie lijnen a', b', c' door een punt M (eventueel L = M), bestaat er precies één projectiviteit ψ van de lijnenwaaier L op de lijnenwaaier M met ψ(a) = a', ψ(b) = b' en ψ(c) = c'.
Bewijs: Zij p een rechte, niet door L of M. Zij X:=x.p voor x door L, en X ' :=x'.p voor x' door M.
Zij φ de projectiviteit van p op p met φ(A) = A', φ(B) = B', φ(C) = C'.
Zij δ de elementaire perspectiviteit van L naar p, en ε de elementaire perspectiviteit van M naar p. Dan voldoet ψ := ε^-1φδ.
Stel ψ' voldoet ook. Dan is φ' := εψ'δ^-1 een projectiviteit van p op p met φ'(A) = A', φ'(B) = B', φ'(C) = C'. Dus φ = φ'. Maar dan is ψ' = ε^-1φδ = ψ.

O40 Kies twee punten A en B op l, beide ongelijk aan S. Zij A' := φ(A), B' := φ(B), en zij T het snijpunt van AA' en BB'.
Zij ψ de perspectiviteit van l op m met centrum T.
Dan is ψ(A)=φ(A), ψ(B)=φ(B), ψ(C)=φ(C). Volgens FS is ψ = φ.

O41 Als c = a + λ(b - a) dan F(c) = F(a) + λ(F(b) - F(a)), en || (F(c) - F(a))|| / ||(F(b) - F(a)) || = |λ| = || (c - a) || / || (b - a) ||.
Dat F de dubbelverhouding bewaart volgt dan uit het volgende plaatje:

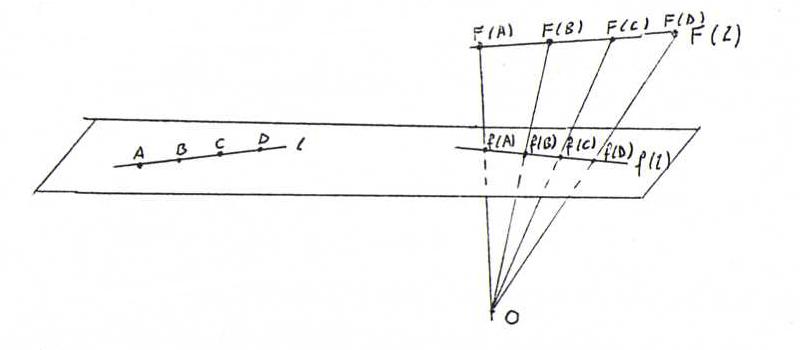
(A, B; C, D) = (F(A), F(B); F(C), F(D)) = (f(A), f(B); f(C), f(D)).
De eerste gelijkheid volgt uit het eerste deel van deze uitwerking, de tweede door projectie uit O.

O42
c = -a + 2b, dus λ= -1, μ=2; c' = (1/2)a' + (1/2)b', dus ρ = σ = 1/2.
Zij x = (0,ξ,1), dan x = (2-ξ)a + (ξ-1)b.
Dus F(x) = (1/2)(ξ-2)a' + (1/4)(ξ-1)b' = ((3-ξ)/4, 0, (3ξ-5)/4). Dus f(x) = ((3-ξ)/(3ξ-5), 0, 1).
We hebben (A, B; C, X) = (2ξ-4)/(ξ-1) en (A', B'; C', X') = (1-ξ')/(1+ξ'). Met ξ' = (3-ξ)/(3ξ-5) volgt (A, B; C, X) = (A', B'; C', X').