PROJECTIVE GEOMETRY COURSE
§ 3: The theorems of Pappus and Desargues
In the real projective plane P2, two theorems hold that can't be deduced from the axioms A1 through A4, so that they don't hold in every model of a projective geometry:
the theorems of Pappus and Desargues.
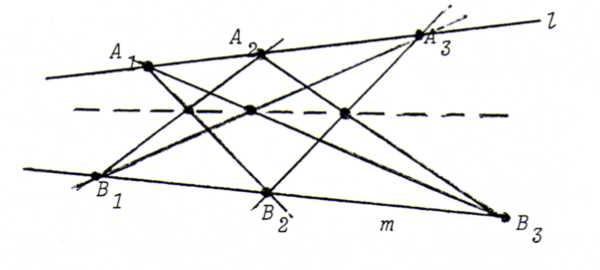
Theorem of Pappus: Given two lines l and m, three points A1, A2 and A3 on l, and three points B1,
B2 and B3 on m. Then the intersection points A1B2. A2B1,
A2B3. A3B2 and A3B1. A1B3 are lying on one straight line.

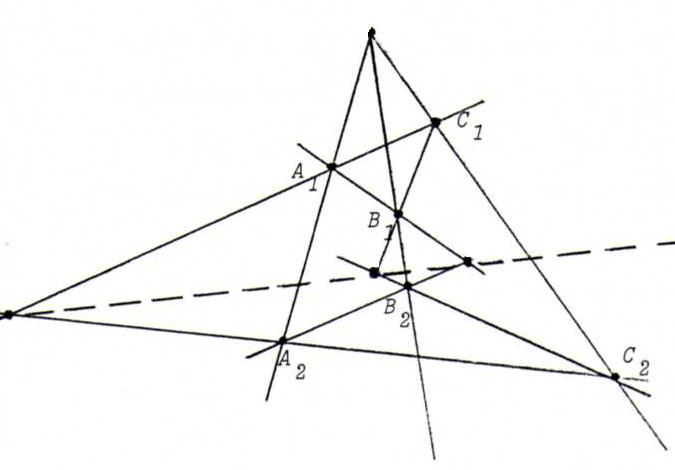
Theorem of Desargues: Given two triangles A1B1C1 and A2B2C2,
where A1A2, B1B2 and C1C2 go through one point. Then the intersection points
A1B1. A2B2, A1C1. A2C2 and
B1C1. B2C2 are collinear.
Another formulation: if two triangles are point perspective, they are correspondingly line perspective.
Remarks:
1. We can prove that the theorem of Desargues follows from the theorem of Pappus. The reverse assertion doesn't hold.
2. We can build up the geometry of the real projective plane by adding to the axioma's A1 through A4 the theorem of Pappus and its dual (synthetic method). We shall not do this, but instead we use
the projective concept cross ratio to prove both theorems. For the proofs, see §11.
3. We can use the theorems of Pappus and Desargues for ruler constructions ("Messung mit dem Richtscheid", Dürer). See O9 and O10.
O8 Dualise the theorems of Pappus and Desargues and make the corresponding constructions.
O9 Given two lines l and m and a point P not on l and not on m, whilst the intersection point l.m isn't in the piece of paper. Construct
the straight line that connects P with l.m. (You can use any of the theorems Desargues, Pappus and dual Pappus.)
O10 Given a line l and two points A en B, not lying on l. Between A and B there is some grease from a candle, so that we can't draw the line
AB.
Construct the intersection point AB.l.
O11 Start from the real projective plane and define a new geometry as follows: points as in P2, lines as in P2, except that lines y=m(x-a)
with positive m are replaced with lines that are broken on the x-axis satisfying y=m(x-a) for x smaller than a, and y=(m/2).(x-a) for x greater than a.
Check that in this geometry the axioms A1 through A4 do hold, but the theorem of Desargues doesn't. (Consider the triangles (-1,0),(1,0),(0,1) and (-1,-2),(1,-2),(0,-1).)
So in this geometry, Pappus doesn't hold either. (See above, remark 1.) Show this with an example.