
PROJECTIVE GEOMETRY COURSE
§ 22: Theory of pole and polar line
Let k be a non-degenerated conic with homogeneous equation xtAx = 0 (so A is symmetric and regular).
Now define for this conic k a bijective mapping from the set of the points in P2 onto the set of the lines in P2 by
P:λp →γ γ(P):λAp .
We have: P ∈ γ(Q) ↔ Q ∈ γ(P), because ptAq = 0 ↔ qtAp = 0

So, if we extend γ by γ(P) →γ P, then we have a bijection from P2 to P2 that maps points to lines,
lines to points, preserves incidence and cross ratio (see O37 and O41), and is involutory, so a polarity.
Henceforth we denote a point and its image line with the same letter: X and x.
In projective coordinates, the polar line of P:λp becomes p:λAp, so the equation of the polar line is p: xtAp = 0. So we find the equation of the
polar line by 'honest distribution'
Therefore we see from the second half of §20 that if P lies on k then the polar line is tangent line. It will appear from the text below that if P is not lying on k then the polar
line doesn't go through P. So, apparently, P is selfconjugated if and only if P lies on k.
If we can draw from P two tangents to k, with contact points Q1 and Q2, we see:
(P ∈ q1 → Q1 ∈ p), en (P ∈ q2 → Q2 ∈ p), so p =
Q1Q2.
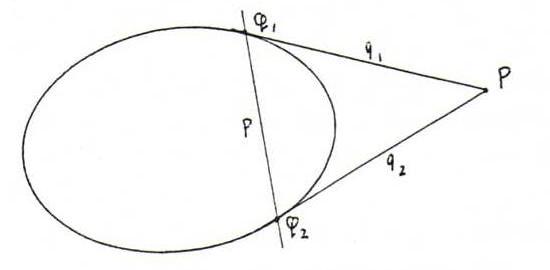
Now look at the sketch below and the corresponding proposition thereafter.
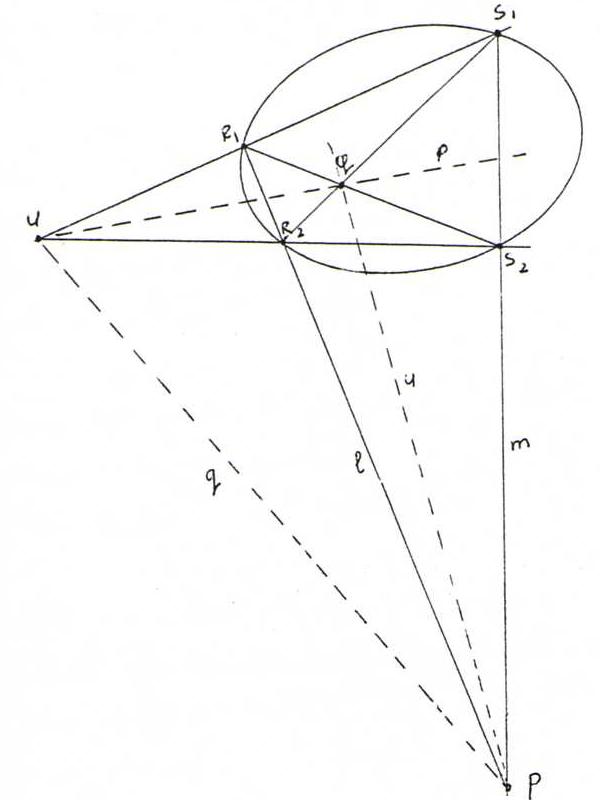
Proposition: If we draw through a point P, not on k, a line l that intersects k in R1 and R2, and a line m that intersects k in S1 and S2, then the diagonal points P, Q and U of the complete quadrangle R1R2S1S2 form a polar triangle.
Proof: According to the last proposition of §19, γ induces on l an involution X → x.l with fixed points R1 and R2, and also
on m an involution with fixed points S1 and S2.
According to the second proposition of §14, P and p.l are then harmonically situated with respect to R1 and R2, and likewise
P and p.m with respect to S1 and S2.
Hence, from the proposition of §12 it follows that p coincides with UQ.
Likewise we prove u = PQ, so q = UP.
Now there are some interesting consequences in the picture: the contact points from the tangents to k through P are lying on QU, the tangents in R1 and S2 intersect on q, etcetera.
O83 Construct the pole of a given line l with respect to a given conic k that has no point in common with l. Taking the intersection point of a line and a conic is allowed in this problem.