Let l and m be two lines in ℜ3 through 0 , with direction vectors l en m.
Let A be a regular linear transformation of ℜ3 with A(l) = m and A(m) = n (n not in the plane spanned by l and m).
On the base l, m, n, the matrix has the form
PROJECTIVE GEOMETRY COURSE
§ 21: Introduction starting from analytic geometry
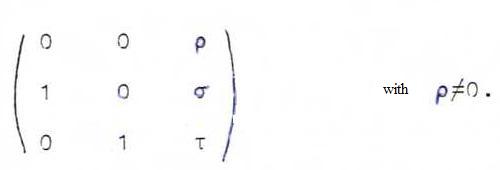
Let l and m be two lines in ℜ3 through 0 , with direction vectors l en m.
Let A be a regular linear transformation of ℜ3 with A(l) = m and A(m) = n (n not in the plane
spanned by l and m).
On the base l, m, n, the matrix has the form

In coordinates with respect to l, m, n, an arbitrary plane through l has equation β y' + γ z'= 0 and vector representation u(1,0,0) + v(0,-γ,β).
A maps this plane onto the plane through m with vector representation u(0,1,0) + v(ρβ, σβ, -γ+τβ) and equation
(γ-τβ)x'+ ρβz'= 0.
We find the geometric locus of the intersection lines of the original plane and its image plane by eliminating β and γ. We get (see O81): x'y' + τx'z' = ρ(z')2.
Now if we take coordinates (x,y,z) with respect to the natural base, via the formula

we find (ax+by+cz)(dx+ey+fz) + τ(ax+by+cz)(gx+hy+iz) = ρ(gx+hy+iz)2.
This is the equation of an arbitrary conic.
This justifies the following projective definition of a conic: a conic is the set of intersection points x.φ(x), where φ is a projective transformation of P2 and x runs through a pencil of lines.
Notice that if n does lie in the plane of l and m, we find three points L, M, N in P2 with φA(L) = M, φA(M) = N, whilst L, M, N are collinear. According to the dual of O40, φA|L is then a perspectivity, so the conic degenerates and becomes two lines (LM and the axis of the perspectivity). We also get degenerations if L = M (determine the kind of degeneration; distinguish between φ = id, φ hyperbolic, elliptic or parabolic).
Proposition: The conic k: xtAx = 0 is degenerated if and only if det(A) = 0.
Proof:
1. Suppose k is degenerated.
If k is one point, the equation has the form (px+qy+rz)2 + (ux+vy+wz)2 = 0. Check that in this case det(A) = 0.
Otherwise, there exist two distinct points P and Q such that the whole line PQ is lying on k. Then (p+aq)tA(p+aq) = 0 for all a, so ptAp = ptAq =
qtAp = qtAq = 0. Then the points λAp and λAq are both lying on the lines with projective coordinates λp and λq respectively, so Ap = μAq.
Then A(p-μq) = 0 whilst p ≠ μq, so det(A)=0.
2. Suppose det(A)=0.
Then Im A is a plane through O or a straight line through O. The vectors Ap with p on k are then lying in one plane. But if k is non-degenerated, Ap is normal vector of the plane through O and the tangent
to k in P. So k must be degenerated.
Remark : There exist empty conics as well, like x2+y2+z2 = 0. For the last one we have A=E3, so det(A) ≠ 0; we call it non-degenerated.
O81 Eliminate β and γ from β y' + γ z' = (γ - τ β) x'+ ρβ z' = 0 (β, γ ≠ 0).
O82 Prove, starting from a1 1x12 + a2 2x22 + a3 3x32 + 2 a1 2x1x2 + 2 a1 3x1x3 + 2 a2 3x2x3 = 0, that through five points there goes in general exactly one conic (if these five points are freely situated, there is exactly one non-degenerated conic that goes through them).