§ 16: The main theorem about collineations

Proposition : Let φ be a projective transformation of P². Then there is a pencil of points that are invariant under φ if and only if there is a pencil of lines that are invariant under φ.

Proof : Suppose there is a point C such that the lines through C are invariant. Let X ' := φ(X). Suppose φ is not the identical mapping.
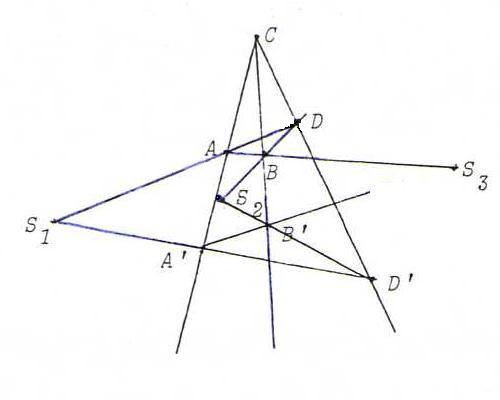
Make a Desargues configuration with centre C and triangles ABD and A ' B ' D ' .

The intersection points S₁, S₂, S₃ of corresponding sides are distinct and according to Desargues collinear.
They are fixed points of φ: for example φ(S₁) lies on CS₁ because CS₁ is invariant, and φ(S₁) lies on A ' D ' because S₁ lies on AD, so φ(S₁) = S₁.
Then the line a through S₁, S₂ and S₃ contains at least three fixed points and hence, according to FT, it is pointwise invariant.

On the other hand, suppose there is a pencil a of invariant points.
We distinguish two cases:
i) There is a fixed point C outside a. In that case, every line l through C contains two fixed points, namely C and the intersection point l.a, so l is invariant.
ii) There is no fixed point outside a. Take a point P outside a. Then P ' lies outside a, too, because φ is 1-1 and a is a line of fixed points.
Now let C := a.PP ' . Then C lies on a, so C is fixed point.
So PC = P ' C = P ' C ' , so PC is an invariant line.
Now take X outside a and outside PP ' . Like PP ' , XX ' is invariant.
So PP ' . XX ' is fixed point and lies therefore on a. Since it also lies on PP ' , it is C.
So the pencil of lines through C is invariant.

Definition : We call a projective transformation, not identity, with a line a of fixed points and a pencil C of invariant lines central collineation with centre C and axis a.

Remark : For the relation between central collineations and central projections, see §4.

Problem 63 : Prove that λ((4,0,-1),(0,3,0),(2,0,1)) is the matrix of a central collineation.
Find the (homogeneous) coordinates of the centre and an equation of the axis.

Problem 64 : Find the matrix of the projective transformation φ defined by
λ(0,1,1) → λ(1,0,0), λ(-1,0,1) → λ(1,1,0), λ(0,7,0) → λ(2,2,2), λ(-2,2,3) → λ(1,0,1).
Does φ have fixed points?

answers