PROJECTIVE GEOMETRY COURSE
Chapter 3: PROJECTIVE TRANSFORMATIONS OF THE PROJECTIVE PLANE
§ 15: Collineations and projective mappings
Definition : A collineation of P2 is a bijection φ from P2 onto itself that maps points to points and lines to lines, whilst
φ(A) lies on φ(l) if and only if A lies on l.
Proposition : Every collineation preserves the harmonic position of pairs of points (and likewise of pairs of lines).
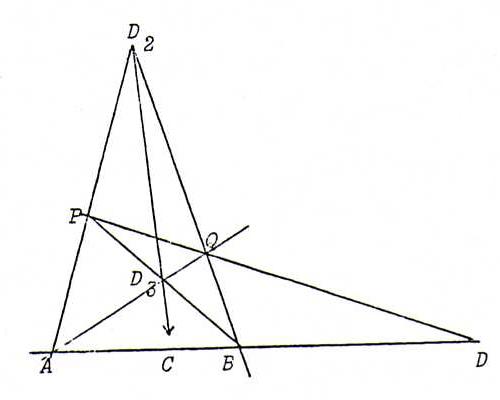
Proof : Let {A,B} and {C,D} be pairs on a pencil of points l that separate harmonically.
Form a complete quadrangle ABPQ with diagonal points D = D1 = AB.PQ,
D2 = AP.BQ, D3 = AQ.BP.
Then we must have C = l.D2D3 (see §12).

If we denote by X ' the image point of X under the collineation, then it turns out that:
quadrangle ABPQ maps to quadrangle A ' B ' P ' Q ' with diagonal points
D1 ' , D2 ' , D3 ' .
So C ' is the fourth harmonic with {A ' , B ' } and D ' .
Definition : A projective mapping from P2 onto P2 is a collineation of P2 that preserves cross ratio.
Remark : The projective mappings are exactly the continuous collineations.
Fundamental theorem : Let A, B, C, D freely situated points in P2, and likewise
A ' , B ' , C ' , D ' . Then there exists exactly one projective transformation of P2 that maps A to A ' ,
B to B ' , C to C ' , and D to D ' .
Proof :
1) unicity : Suppose φ and ψ meet the requirements. Then φψ-1 is a projective mapping with four freely situated fixed points, so identity (see O59). Dus φ = ψ.
2) existence : Use projective coordinaten. Represent X in P2 by λx with x ∈ ℜ3.
Fix x by the further demands ||x|| = 1, x1 + x2 + x3 positive.
Now let α, β, γ ∈ ℜ be determined by d = αa + βb + γc (αβγ≠0).
Let ρ, σ, τ ∈ ℜ be determined by d ' = ρ(αa ' ) + σ(βb ' ) +
τ(γc ' ) (ρστ≠0).
Let P be the linear transformation of ℜ3 defined by P(a) = ρa ', P(b) = σb ',
P(c) = τc '.
Then P(d) = d ', and P induces on P2 a collineation as required.
Now see O61 for the sequel.
Remark : From the proof under 2) above and O61 we see that each projective transformation of P2 is induced by some regular linear
transformation of ℜ3 (and by each λ-tuple thereof , λ ≠ 0).
We used this in §6.
Problem 59 : Prove that every projective transformation with four freely situated fixed points is identity.
Hint: Start from the complete quadrangle ABCD of the fixed points, and use the propositions of §10.
Problem 60 : Let φ be a projective transformation of P2. Let L be a point in P2.
Prove that φ induces a projectivity from the pencil of lines L onto the pencil of lines L ', with L ' = φ(L).
Provre also that φ is identity if φ leaves two pencils of lines linewise linvariant. Dualise.
Problem 61 : Let P be a regular linear transformation of ℜ3.
Prove that P preserves the collinearity of any three points A, B, C on a line l, : AB/AC =
P(A)P(B)/P(A)P(C).
Prove subsequently that the collineation φ, induced by P on P2, preserves cross ratio.
Problem 62 : Consider four freely situated points A, B, C, D, and four freely situated points A ' , B ' , C ' , D ' .
Construct the image point of an arbitrary point X under the projective transformation that maps A to A ', B to B ', C to C ' , and
D to D ' .
(Hint: project D from every vertex of the triangle ABC onto the opposite side. Do the same with D ' and A ' B ' C ' . Now reduce the construction to
the projectivities induced the sides ofn ABC and use Steiner.)