PROJECTIVE GEOMETRY COURSE
§ 13: Three kinds of projectivities from a line onto itself
Remark : If φ is a projectivity from a pencil of points l onto itself, and φ has three fixed points, then φ is identity.
This follows from the fundamental theorem.
Likewise: a projectivity from a pencil of lines L onto itself with three invariant lines is identitity.
Definition : Let φ be a projectivity from a pencil of points l onto itself (respectively from a pencil of lines L onto itself).
i) If φ has no fixed points (invariant lines), then we say φ is elliptic.
ii) If φ has exactly one fixed point (invariant line), we say φ is parabolic.
i) If φ has two fixed points (invariant lines), we say φ is hyperbolic.
There exist projectivities of each kind:
i) Let φ be the projectivity l → l with, for three given points A, B, C on l, φ(A) = B, φ(B) = C,
φ(C) = A.
Supoose there is a fixed point D. Then (A, B; C, D) = (B, C; A, D), so d = 1 - 1/d (vgl O36). Since for all real
numbers d, and also for d=∞, we have d ≠ 1 - 1/d, we find a contradiction.
So φ is elliptic.
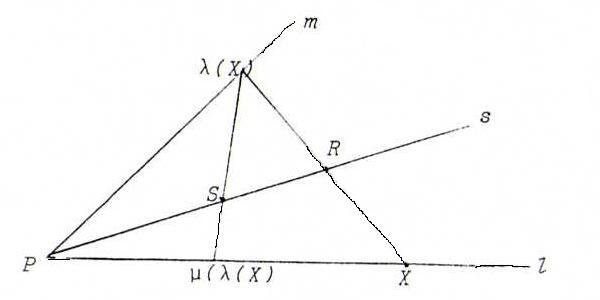
ii) (see the picture below)

Let λ be the perspectivity from l onto m with center R, and μ the perspectivity from m onto l with center S.
Then μoλ is a parabolic projectivity from l onto l (P is the only fixed point).
Make the dual construction, too.
iii) Let A, B, C, D be distinct points on l. Let φ be the projectivity l → l with φ(A) = A, φ(B) = B, φ(C) = D. Dan is φ niet de identieke afbeelding, maar φ heeft wel twee verschillende dekpunten. Dus is φ hyperbolisch.
Using the third proposition of §10, show that the projectivities from a line l onto itself correspond to the regular 2 by 2 matrices.
How can we determine for a given matrix A what the kind of the corresponding projectivity is?
Do the parabolic projectivities, plus identity, form a subgroup of the group of projectivities from l onto l?
O52 Suppose we have a hyperbolic projectivity π with π(A) = A, π(B) = B', π(C) = C'.
Construct the second fixed point.
O53 Let π be a parabolic projectivity with fixed point A, and let π(B) = B'. Construct the image point of X.
O54 Given a line l: λ(1,2,1) with on it the points A: λ(2,-1,0), B: λ(0,1,-2), and C: λ(-1,1,-1).
Let φ be the projectivity from l onto l that maps A to itself, and B and C in each other.
Give the matrix of φ on the base b, c, and find the fixed points of φ.