COURSE OF PROJECTIVE GEOMETRY
EP: hints:
1.
a) ψ is the product of the elementary perspectivities from l via A and K and B onto l, then the restriction to l of the polarity, and finally the
elementary perspectivity from L onto l.
b) Make a picture, and show that each of C, D and O: λ(0,0,1) is mapped to itself. Since ψ has three fixed points, ψ is identity.
c) (Simple. For the construction of the polar line, see §22.)
d) Check that C and D are always fixed points.
e) If X = AE . l, then SX = E. Now let Y = BSX . l.
Construct the other intersection point Z of AY and K using Pascal. Then y is the diagonal of ABEZ that doesn't go through Y, and
ψ(X) = y . l.
f) (The same as the answer to O102, fragment Kaper-Westerman; for J, take a circle.)
g) X : λ(0,√2-1,1) with ψ(X) = λ(0,(1/2)√2,1). Now construct a 3 by 3 matrix that maps (0,√2-1,1) to a scalar multiple of
(0,(1/2)√2,1), and maps each of (0,1,1) and (0,-1,1) in a scalar multiple of itself.
2. π is the product of the restriction to l of the polarity related to K and the elementary perspectivity from L onto m.
If p is the Pappus line, then π(l . m) = p . m and π(l . p) = l . m.
So LM . m = p . m and LP . m = l . m.
So LM goes through p . m and (since l . m lies on LP) through l . p.
So p = LM.
3. If A, B, C, D, E are the given points, we can take for φ the projectivity between pencils of lines from A to B that maps
AC to BC, AD to BD, AE to BE. The intersection points we have to construct are the fixed points of the projectivity induced on l.
We can construct these using an auxiliary circle as in the fragment Kaper-Westerman in the answer to O102.
4. Let A, B, C, D be the given proper intersection points, and O the given point at infinity.
Construct the perpendicular to AO from A. Let S be the other intersection point of this perpendicular and the conic. Construct S by applying Pascal to hexagon ABC-DOS.
Construct the perpendicular on [AS] that goes through the middle of [AS]. This line goes through O and the top T we have to construct. Construct T by applying Pascal to
hexagon AOD-CBT.
5. We can do this using the methode of the false positions. (See the answer to O102.) So:
Start with an arbitrary point X on l. Connect this point with A and intersect the connecting line with the line at infinity. Connect this intersection point at infinity with
C and intersect the connecting line with m. Connect this intersection point with D and intersect the connecting line with the line at infinity. Connect this intersection point at
infinity with B and intersect the connecting line with l. Call this last intersection point X '.
The mapping X → X ' is a projectivity from l onto itself. Construct for two more points X the image point X '.
Now construct the fixed points of this projectivity, as in the first fragment of the answer to O102. (Use for J a circle, then it's still a construction with compasses and ruler.)
There are zero or one or two fixed points.
If we begin with a fixed point X, then the construction produces a solution to the problem (and also the point Y on m).
6.
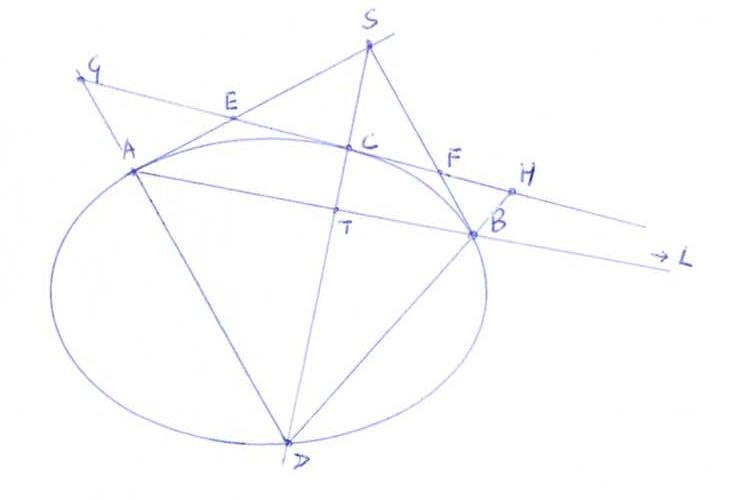
L ∈ s ⇒ S ∈ l
L ∈ c ⇒ C ∈ l
So l = SC (and LD is tangent to K in D).
So if T := AB . SC, then {L, T} and {A, B} separate harmonically.
By projection from S we then see that {L, C} and {E, F} separate harmonically.
By projection from D we then see that {L, C} and {G, H} separate harmonically.
Let J be the conic through A, B, D, E and F.
Because of the first and second of the forementioned harmonic situations, SC is also polar line of L with respect to J. Since D lies on this polar line, L
must lie on the tangent to J in D.
So LD is tangent to both K and J in D.
7. A conic, because φ is a projectivity and induces a projectivity from A onto B. In concrete cases, we can simply construct the conic point after point.
8. The polar line of the top is the tangent x2 = 0 with projective coordinates λ(0,1,0). The polar line of the point at infinity on the axis is the tangent x3 = 0 with
projective coordinates λ(0,0,1).
The intersection point of these two tangents is the point at infinity on x2 = 0, so λ(1,0,0). So that's the pole of the axis of the parabola.
9. K is generated by φ : A → B with φ(AS) = BS, φ(AT) = BT, φ(AC) = BC.
K ' is generated by ψ : A → B with ψ(AU) = BU, φ(AV) = BV, ψ(AC) = BC.
Construct ψ-1(BS) and ψ-1(BT) using the theorem of Steiner.
Thus we find three images of θ := ψ-1φ : A → A, namely the images of AS, AT and AC (the last one is invariant). If we find yet another
invariant line x, then φ(x) = ψ(x), so x . φ(x) = x . ψ(x), so this then yields a fourth
intersection point of K and K '.
We can construct such a second invariant line as follows:
θ induces on an arbitrarily chosen line l that doesn't go through A a projectivity ω := ε-1θε where ε is the elementary perspectivity
of connection from l onto A. So we also know a fixed point and two other pairs of point and image point of ω. In general there is one more fixed point (otherwise, K and K '
are tangent or they coincide). Construct this second fixed point as in O52.
10. Apply Brianchon to d b α - a δ c. Then we see that α . δ lies on the fixed line ((D-(a . b)) .
(A-(c . d))) - (b . c).
11. If we apply Pascal to A C D1 - D B A1 and to B1 C D1 -
C1 B A1, we see that CA1 . BD1 lies on OL and OM.
12.
a) If we apply Brianchon to a b c - c a b .
b) If we apply Brianchon to a b c - b a l, then we see that the lines A1B1 all go through
((b . l) - (a . c)) . ((a . l) - (b . c)) .
c) AA1 → BB1 is a projectivity from A onto B (it's the product of the elementary perspectivity from A onto BC, the perspectivity
of part b) from BC onto AC, and the elementary perspectivity from AC onto B).
This projectivity φ induces the conic mentioned in the problem.
This conic goes through A and B and, since φ(AC) = BC, also through C.
HOME
