§ 9: answers

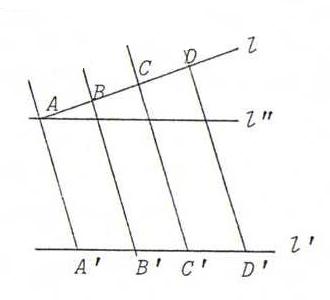
O35

i) P at infinity, D proper.
Draw a help line through A parallel to l'.

ii) P, D, D' at infinity.
As i), but now we have only to prove AC/BC = A'C'/B'C'.

iii) D at infinity, P proper.
This is the limit of the general case.

iv) l line at infinity.
In this case, the proposition follows from the definition of the cross ratio of four points on the line at infinity.

O36
1 2 3 4   λ    2 1 3 4   μ    3 1 2 4   ν    4 1 2 3   ρ
1 2 4 3   μ    2 1 4 3   λ    3 1 4 2   σ    4 1 3 2   τ
1 3 2 4   σ    2 3 1 4   τ    3 2 1 4   ρ    4 2 1 3   ν
1 3 4 2   ν    2 3 4 1   ρ    3 2 4 1   τ    4 2 3 1   σ
1 4 2 3   τ    2 4 1 3   σ    3 4 1 2   λ    4 3 1 2   μ
1 4 3 2   ρ    2 4 3 1   ν    3 4 2 1   μ    4 3 2 1   λ

where μ=1/λ, ν=1/(1-λ), ρ=λ/(λ-1), σ=1-λ, τ=1-1/λ.

O37 If X₁, X₂, X₃, X₄ are four points on a line l, and x₁, x₂, x₃, x₄ four lines such that x_i has the same projective coordinates as X_i, then x₁, x₂, x₃, x₄ go through one point L with the same projective coordinates as l:

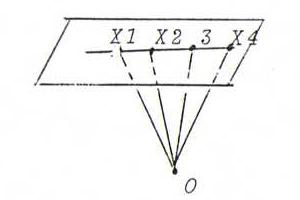
x_i is the line of intersection of x₃=1 and the plane α_i through O whose normal is OX_i; these four planes go through the normal of the plane through O and l.
Let Y_i := l.x_i ; then ∠X_iOY_i = 90 degrees. From this it follows that (x₁, x₂; x₃, x₄) = (Y₁, Y₂; Y₃, Y₄) = (X₁, X₂; X₃, X₄).

O38 Consider the line as an axis of the real numbers, so f(x) = E(x-c)/(x-d) with E=(b-d)/(b-c). Draw the graph of f.
For each point of l (proper or at infinity), there exist a vicinity V of the image of that point and a vicinity U of the point itself such that if Y ∈ U then f(Y) ∈ V.