§ 6: answers

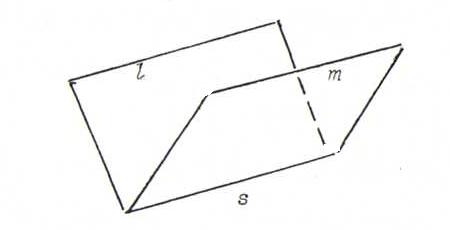
O22 Let l and m be lines in P², corresponding with planes α and β through 0 in ℜ³. We call l and m parallel if they intersect in a point at infinity (so if the intersection line s of α and β lies in γ:{x₃=0}).

If we take a projective transformation φ, which comes from the regular linear transformation A, then φ(l) and φ(m) are parallel if and only if A(s)⊂γ, so if and only if A is affine as well.
Indeed, A(α)∩A(β) = A(α∩β) = A(s), and φ(l) and φ(m) are parallel if and only if A(α)∩A(β) lies in γ.

O23 The angle θ between two lines l and m in x₃=1 is invariant under the similarity stransformation that comes about if we first project perpendicular to x₃=0, then apply in x₃=0 a rotation or reflection, multiplied with a scalar ρ, and finally translate over (a,b,1).
Also, if ρ=1, then the distance between two points in x₃=1 is preserved under the composition of these three mappings.

O24
Complete quadrilateral: P, A, G, C; parallellogram: A, G, C; rhomb and square: G, C.

For example, take the points (0,0,1), (1,0,1), (0,1,1) and (1,1,1) in x₃=1, the vertices of a square.
Let A be the regular linear transformation of ℜ³ with matrix rows ((1,1,1),(0,0,1),(1,0,1)).
Then under A, (0,0,1) → (1,1,1), so φ(0,0,1)=(1,1,1); likewise (1,0,1) → (2,1,2), so φ(1,0,1)=(1, 1/2, 1); likewise (0,1,1) → (2,1,1), so φ(0,1,1)=(2,1,1); likewise (1,1,1) → (3,1,2), so φ(1,1,1)=(3/2, 1/2, 1).
So the image under φ of this square isn't even a parallellogram.
Apparently, the concepts square, rhomb and parallellogram are not projective.

O25 No. Definer a hyperbola as a conic that intersects the line at infinity L_∞ in two points. Example: H with inhomogeneous equation xy=1, homogeneous equation xy=z²; the points at infinity S:λ(1,0,0) en T:λ(0,1,0) are lying on it.

Now let φ be an affine transformation, which comes from the regular linear transformation A of ℜ³.
Then {A(S), A(T)} = A(H∩L_∞) = A(H)∩A(L_∞) = A(H)∩L_∞, so A(H) intersects L_∞ in two points, too. We see that an affine transformation maps each hyperbola onto a hyperbola.
So a hyperbool and an ellipse can't ever be A-equal.

O26 (A,B;C,L_∞) = AC/BC, so:
i) (A,B;X,L_∞) smaller than 0;
ii) (A,B;C,L_∞) ∈ {4,-2};
iii) (A,B;C,L_∞) = -1.