§ 27:

O102

Fragment from Kaper-Westerman:

Note 3.5.1:

This yield the possibility to 'construct' the fixed points of a projective mapping φ from a line l onto itself.
Suppose a conic J has been drawn. Let φ be given by three points A, B, C and their images A', B', C' on l.
Take a point S on J and let A, B, C, A', B', C' be the projections of A, B, C, A', B', C' on J from S.
Let ψ be the projectivity from J onto itself determined by A, B, C and their image points A', B', C'.
If the axis of J intersects J, then the projections of the intersection points from S on l are the fixed points of φ.

Fragment from "An introduction to Projective Geometry" by Daniel Pedoe:

3. The method of false positions.

If we have only three pairs of corresponding points on a line, the projectivity from the pencil of points on this line onto itself whereof these pairs are pairs of point and image point is uniquely determined and can have 0, 1 or 2 fixed points.
There is a class of problems, first introduced by Poncelet, whose solutions depend on the existence and the construction of such fixed points.
The following is a typical example:

To construct a quadrilateral so that the four sides go through four given points and the four vertices go through four given lines.

Let A, B, C, D be the given points and l₁, l₂, l₃, l₄ the four given lines.
Draw any line through A, intersecting l₁ and l₂ in P₁ and P₂.
Draw BP₂, which intersects l₃ in P₃.
Draw CP₃, which intersects l₄ in P₄.
Draw DP₄, which intersects l₁ in P'.
This procedure determines a projectivity φ from l₁ onto itself with φ(P₁) = P'.
Now if we find the fixed points (0, 1 or 2) of this projectivity φ, this gives us 0, 1 or 2 solutions of the problem.

Because the production of three pairs of corresponding points requires the construction of three quadrilaterals that aren't close-fitting and, hence, don't yield a solution of the problem, the method is called 'the method of false positions'. Three constructions that are false because they don't solve the problem give the material we need to solve the problem.

O103 Begin with three points P₁, P₂, P₃ on AB and find by projection from U on BC the points Q₁, Q₂, Q₃. Then, find by projection from V on AC the points R₁, R₂, R₃. Finally, find by projection from W on AB the points P₁ ', P₂', P₃'.

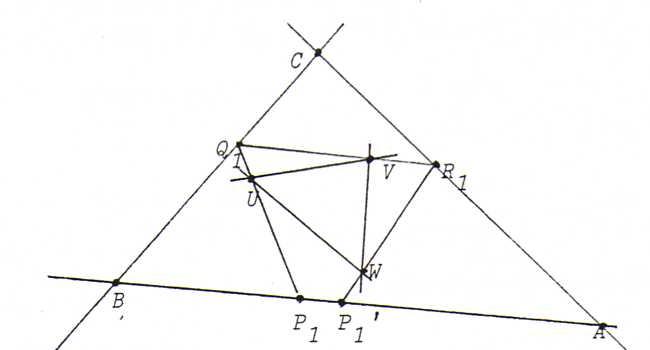
We can use the fixed points of the projectivity with φ(P_i)=P_i' as starting points P for a close-fitting trianglePQR.