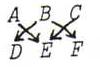
 has a Pascal line which goes through AE.BD, AF.CD, BF.CE.
has a Pascal line which goes through AE.BD, AF.CD, BF.CE.
If you didn't know this yet, you have to study the answers again.
COURSE OF PROJECTIVE GEOMETRY
§ 26:
O96
Apply Pascal to hexagon
ABC
BAD .
O97
Let P ' be the point from which the triangles are perpective. We have to prove P ', X, Y are collinear and P ', X, Z are collinear.
Apply Pacal to
A2C1B2
B1P A1
and to
B1C2A2
P A1C1
O98
If A, B, C, D, E are the given points, and X the second intersection point of J and an arbitrary line l through A,
then we construct X by applying Pascal to
ABC
DEX.
So letP := AE.BD, and Q := AX.CD = l.CD, and t := PQ. Then R := BX.EC =
t.EC. So X := l.BR.
O99
For X on J, let x be the tangent to J in X, so the polar line of X.
For X, Y in {A, B, C} is x.y ' the pole of XY ' , so x.y ' - x '.y the polar line of
XY '.YX '.
So the point P that lies on the three lines x.y ' - x '.y, is the pole of the line p on which the three points XY '.YX '
are lying.
O100
Let A, B, C, D be the four given points, and a the given tangent. Construct the tangent in B by applying Pascal to
ABC
DAB.
So: let P := AA.BD = a.BD, Q := AB.CD, t := PQ.
Then the tangent to J in B goes through t.AC.
O101
Ad O88: apply Pascal to
ABC
DAE.
Ad O90: Construct the Brianchon point P of hexagon
abc
cab.
The point of contact we have to construct, c.c = C, is collinear with P and a.b.
Note: The order of the points in the hexagon is important:
 has a Pascal line which goes through AE.BD, AF.CD, BF.CE.
has a Pascal line which goes through AE.BD, AF.CD, BF.CE.
If you didn't know this yet, you have to study the answers again.