COURSE OF PROJECTIVE GEOMETRY
§ 25:
O92
Proof that the hint is valid:
Let S := a. x. Let a and a ' be the tangents to J through S. We assume a ≠ a '. Let A and A ' be the
points of contact on a and a ', respectively.
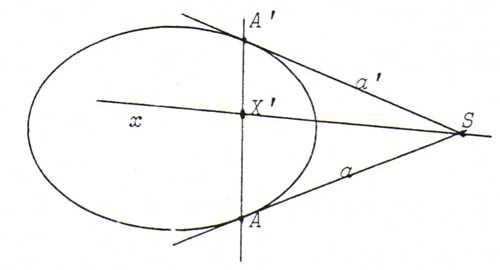
Since S lies on x, X lies on s (= AA ' ), the polar line of S.
Since X and X ' = s. x form a pair that's harmonically separating {A , A ' }, SX and x form a pair that's harmonically separating
{a , a ' }.
Construction:
S := a. x. Construct a ' using O86. Construct the fourth harmonic y with x and {a , a ' }.
Let T := b. x, and let b ' be the other tangent to J through T. Let z be the the fourth harmonic with x and {b , b ' }.
Then X := y.z .
O93 Let b be the polar line of B, so that C lies on b.
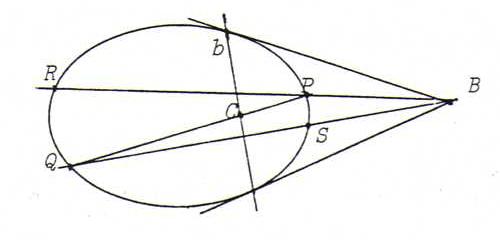
We have to prove: C = PQ.RS.
Proof: Let T := PQ.RS and U := RQ.PS. Then b = UT (see §22). So T = PQ.b = C.
O94 A diagonal of quadrilateral abcd is the line connecting opposite intersection points, for example a.d and b.c .
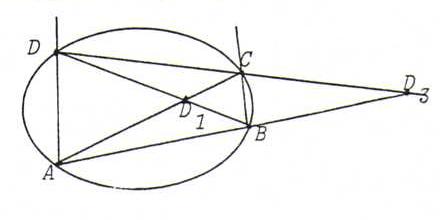
Since a.d and b.c lie on D1D3, etcetera, quadrangle ABCD and quadrilateral abcd have the same diagonals.
HOME


