§ 23:

O84
If L=M, the conic degenerates and becomes a point, a pair of lines or a double line.
If the projectivity is a perspectivitys, the conic degenerates and becomes a pair of lines (LM and the axis of the perspectivity).

If l=m, the conic degenerates and becomes a line or a pencil of lines or a double pencil of lines.
If the projectivity is a perspectivity, the conic degenerates and becomes a pair of points (l . m and the eye of the perspectivity).

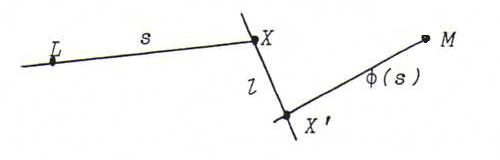
O85
For X on l we construct X ' using the construction of Steiner (see §11). XX ' is a line of the required conic of lines.
If we take X = l . p then we find X ' = l . m . So l belongs to the conic of lines.
If we take X = l . m then we find X ' = p . m . So m belongs to the conic of lines.

O86
Call the lines l, m, a, b, c.
Let A = l . a , B = l . b, C = l . c , A ' = m . a , B ' = m . b, C ' = m . c .
Then the conic originates from the projectivity that maps A to A ' , B to B ' , and C to C ' .
Take X on l and construct X ' using the construction of Steiner. Then XX ' is a sixth line of the conic of lines.

O87
The conic exists of the points x . φ(x), where φ is a projectivity from the pencil of lines L onto a pencil of lines M.
This projectivity induces on every line l (not through L or M) a projectivity θ : X → φ(XL) . l .

If l contains three points of k, then these are the fixed points of θ, and θ is identity. But then φ is a perspectivity with axis l, and k is degenerated.
If l is a line through L, then m . k contains besides L only l . φ(l), or φ(l) = l and k is degenerated.