§ 14:

O55 Suppose A = ((a,b),(c,d)) meets the requirements. A maps (4,-5) to ρ(1,2) and (1,2) to σ(4,-5). We get A = μ((2.1),(-1,-2)).

O56 Suppose A = ((a,b),(c,d)) meets the requirements. Using A² = λE, we find a² = d² and c(a+d) = b(a+d) = 0.
If a=d≠0 then b=c=0, but then the projectivity is trivial. So a=-d.
We find the eigenvalues by equating the characteristic polynomial λ² - a² - bc to 0. So hyperbolic if a² + bc is positive, elliptic if a² + bc is negative. If a² + bc = 0, then the matrix is singular.

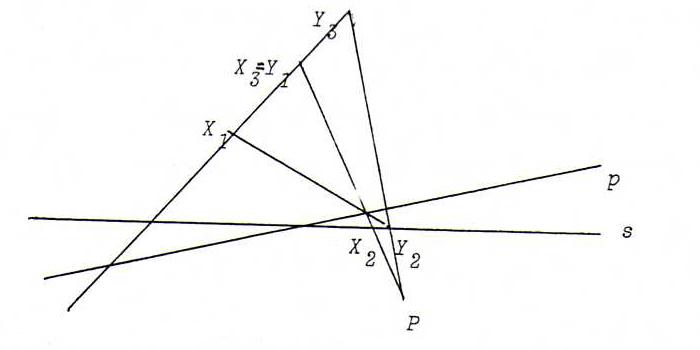
O57 Rename X₃=Y₁ and prove: Y₃=X₁ ↔ P on p.

(Y₃=X₁ ↔ PY₃=PX₁ ↔ Y₂X₁=PX₁)

"→" : If Y₃=X₁ then Y₂X₁=PX₁ and Y₂X₁.Y₁X₂ = PX₁.PX₂ = P. So P on p.

"→" : If P on p then P = p.Y₁X₂ so P op Y₂X₁. Then Y₂X₁=PX₁ so Y₃=X₁.

O58 From the data it follows that (P, Q; A, A') = (P, Q; B, B') = -1 = (Q, P; B, B').
Hence, the projectivity that maps P to Q, and Q to P, and A to B, maps A' to B'.
(It is an involution because it interchanges P and Q.)