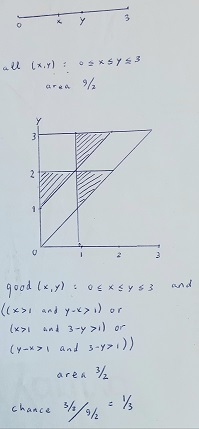
Problem 2019-1/A

Three gamblers select a non-negative probability distribution with mean 1. Say these distributions are F,G,H. Then x is sampled from F, y is sampled from G, z is sampled from H. Biggest number wins. What distributions should the gamblers choose?

Solution:

At first sight it doesn't matter which distributions with mean 1 the gamblers choose, because the expectation value is always 1.
However, if X chooses the distribution F that yields the sample x = 1 with certainty, and Y and Z both use the distribution that yields each of the samples 0.1 and 1.9 with chance 1/2, then the chance that X wins is only 1/4.
To guarantee that the chance of winning solo is at least 1/3, the gamblers have to choose distributions that yield big samples with a relatively big chance and equal samples with zero chance.
So each of them might best choose a continuous distribution E whose density function e(x) is slowly decreasing.
I propose they choose e(x) = a/(x+b)^2+c for some c > 0.
From ∫₀^∞ e(x) dx = 1 = ∫₀^∞ x*e(x) dx we deduce b = c and a = (c+1)c^c+1. Remark e(0) = (c+1)/c.
For c > 1 the variance is finite and equal to (c+1)/(c-1), which descends to the limit 1 if c tends to ∞.
The 50-percentile is c*2^1/(c+1)-c, which ascends to the limit ln(2) = 0.69315.. if c tends to ∞.
So each gambler may choose some c for which the variance is not too big nor too small and the 50-percentile is not too small and the calculating facilities not too troublesome.
If they should agree to choose the same c, for instance c = 10, then each of them only has to take a random sample r from (0,1), because the sample s is found from the equation ∫₀^s e(x) dx = r, so the largest s comes from the largest r.

Problem 2019-1/B

For given m ≥ 3, consider the regular m-gon inscribed in the unit circle. We denote the area of this m-gon by A_m. Suppose m is odd. Prove that 2A_m and A_2m have the same minimal polynomial.

Solution:

We find A_m = (m/2)*sin(2π/m).
Let y₁ = A_2m = m*sin(π/m) and y₂ = 2A_m = m*sin(2π/m). Let x₁ = m*cos(π/m) and x₂ = m*cos(2π/m).
According to de Moivre, (cos(φ) + i sin(φ))^k = cos(kφ) + i sin(kφ), so Im(x₁ + i y₁)^m = 0 and Im(x₂ + i y₂)^m = 0.
Moreover, since m is odd, none of these last two equations holds for an exponent less than m.
But both for x + iy = x₁ + i y₁ and for x + iy = x₂ + i y₂ we have also
Im(x + i y)^m = Im (Σ_k=0^m (m over k) x^m-k (iy)^k) = m yx^m-1 - (m over 3) y³x^m-3 + ... ± y^m, where the exponents of x are all even.
Using cos² = 1 - sin², we can turn this into y times the minimal polynomial p(y) over the rationals, which is the same for y = y₁ and y = y₂.
For instance, for m=3 we get p(y) = 27 - 4y² and for m=5 we get 3125 - 500y² + 16y⁴.

Problem 2019-1/C

Let n be a prime number. Show that there are no groups with exactly n elements of order n. What happens with this statement if n is not a prime number?

Solution:

We deal with the general case at once, so let n have prime factorization p₁^a1...p_k^ak with p₁ ≤ ... ≤ p_k. Let φ denote Euler's totient function.
Suppose a group G contains an element x of order n. Then x generates a cyclic subgroup C of G that contains exactly φ(n) elements of order n, which generate the same subgroup C.
If G contains another element y of order n, outside C, then y generates a cyclic subgroup D of G that has only elements of order less than n in common with C. Etc.
So the union of all these cyclic subgroups of order n, if finite, contains mφ(n) elements of order n for some natural m.
This number mφ(n) is equal to n iff m(p₁-1)..(p_k-1) = p₁..p_k.
Comparing the number of factors 2 at the left and right hand sides, we establish p₁ = 2 and k ≤ 2. If k=2 then by comparing the number of small prime factors at the left and right hand sides, we establish that p₂ must be 3.
We now distinguish between the cases k=1 and k=2.
1) Let k=1, so n = 2^a and m=2. So there are exactly two cyclic subgroups of order 2^a.
First suppose a=1. If the two cyclic subgroups of order 2 are generated by x and y, respectively, then there must be a third cyclic subgroup of order 2, generated by xy=yx. Contradiction. Here we finish the first part of the problem.
Next suppose a>1. There are several groups with 4 elements of order 4, for instance the direct product of C₄ and C₂, where C_s is cyclic of order s.
2) Let k=2, so n = 2^a3^b and m=3. There are several groups with 6 elements of order 6, for instance the direct product C₃*C₂*C₂.
So the statement in the problem holds if n is prime, but not in general.

Problem 2019-2/A (edited)

Let A = (a_i,j ) be the matrix on the natural base e in threedimensional euclidean space of a rotation R (not equal to identity). Suppose none of a_2,3+a_3,2, a_1,3+a_3,1, a_1,2+a_2,1 is 0.
Prove that (1/(a_2,3+a_3,2), 1/(a_1,3+a_3,1), 1/(a_1,2+a_2,1)) is a direction vector of the axis of R.

Solution:

There is an orthonormal base b, whose first vector is eigenvector of R with eigenvalue 1 and direction vector of its axis, so that the matrix of R on base b is [R]_b,b = M with matrix elements m_1,1 = 1, m_1,2 = m_1,3 = m_2,1 = m_3,1 = 0, m_2,2 = m_3,3 = cos(u), m_3,2 = - m_2,3 = sin(u) for some u ∈ (0,2π).
The last two vectors of b may be rotated around the axis over an arbitrary angle without changing this matrix M. This will come in handy.

The relation between A and M is given by the formula A = [R]_e,e = [I]_e,b [R]_b,b [I]_b,e = S M S^-1, where I is identity and the columns of S are the coordinates of the vectors of b on the natural base e and S^-1 is the inverse of S. Since b is orthonormal, S^-1 is the transposed of S.

So we can express each matrix element a_i,j of A in cos(u), sin(u) and the matrix elements s_m,n of S.
Now we have to prove that s_1,1(a_2,3+a_3,2) = s_2,1(a_1,3+a_3,1) = s_3,1(a_1,2+a_2,1).
We may check these identities by taking the last two vectors of basis b in such a way that for some v,w ∈ [0,2π) we have
s_1,1 = cos(v)cos(w), s_1,2 = - sin(v)cos(w), s_1,3 = - sin(w),
s_2,1 = cos(v)sin(w), s_2,2 = - sin(v)sin(w), s_2,3 = cos(w),
s_3,1 = sin(v), s_3,2 = cos(v), s_3,3 = 0.

Problem 2019-2/B (adapted)

1) Let k be a nonnegative integer and X a collection of infinite sets of positive integers such that no two sets of X share more than k positive integers. Prove that X is countable.

2) Does there exist an uncountable collection X of infinite sets of positive integers such that for all distinct sets A and B of X the intersection of A and B is finite?

Solution:

1) For every A in X, let A' be the set containing the smallest k+1 elements of A.
Let X' be the collection of all sets of k+1 positive integers.
Then A → A' is 1-1, so X is countable if X' is countable.
And we can count the sets A' of X' according to the principle: the greater the sum of the elements of A', the greater its number in the count.

2) Yes: take the collection X of all infinite sets of the form {a₁, a₁a₂, a₁a₂a₃, a₁a₂a₃a₄, ... }, where a_i ∈ {0,1,2,...,9} (a₁ > 0) and we use the decimal representation, so for instance 1000 ≤ a₁a₂a₃a₄ ≤ 9999, etc.
We can prove that X is uncountable with the well-known Cantor diagonal argument. In fact {a₁, a₁a₂, a₁a₂a₃, a₁a₂a₃a₄, ... } → Σ a_i 10^-i is (almost) a bijection from X to [0.1,1].
The intersection of two distinct sets of X, if not empty, has always the form {a₁, a₁a₂, ... , a₁a₂..a_k} for some positive integer k, so is always finite.

Problem 2019-4/A

Let F be a monic polynomial of degree 4 with integer coefficients. Let A be a set of integers with at least 5 elements such that for all a ∈ A holds that 2²⁰¹⁹ divides F(a).
Prove that there exist distinct elements a,a' of A such that 2²⁰² divides a - a'.

Solution:

We will show that we can even replace 202 by 504. Indeed, suppose distinct elements a,a' of A such that 2⁵⁰⁴ divides a - a' don't exist. We will derive a contradiction as follows:

Suppose F = x⁴ + px³ + qx² + rx + s.
There exist 5 elements a_i of A, i = 1,2,..,5 , such that 2²⁰¹⁹ divides a_i⁴ + pa_i³ + qa_i² + ra_i + s.
So by subtracting we find 10 pairs i,j such that 2²⁰¹⁹ divides (a_i - a_j)(a_i³ + a_i²a_j + a_ia_j² + a_j³ + pa_i² + pa_ia_j + pa_j² + qa_i + qa_j + r), so 2¹⁵¹⁵ divides a_i³ + a_i²a_j + a_ia_j² + a_j³ + pa_i² + pa_ia_j + pa_j² + qa_i + qa_j + r.
Again by subtracting we find 10 triples i,j,k such that 2¹⁰¹¹ divides a_i² + a_j² + a_k² + a_ia_j + a_ia_k + a_ja_k + pa_i + pa_j + pa_k + q.
Again by subtracting we find 5 quadruples i,j,k,m such that 2⁵⁰⁷ divides a_i + a_j + a_k + a_m + p.
Again by subtracting we find that 2³ divides 1. Contradiction.

Problem 2019-4/B

1. Let n be a positive integer, at least 2, and S a non-empty subset of {1,2,...,n-1}. Prove that there exists a n-th root of unity z such that the real part of Σ_s∈S z^s is at most -1/2.
2. Suppose n is not a power of 2. Prove that there exists a non-empty subset S of {1,2,...,n-1} such that for all n-th roots of unity z the real part of Σ_s∈S z^s is at least -1/2.

Partial solution:

1. Let z = exp(2πik/n) = cos(2πk/n) + i sin(2πk/n) where 0 ≤ k < n. Choosing z amounts to choosing k.
If n = 2 then z = -1 satisfies the requirement.
If n ≥ 3 suppose there is a S so that for each k the real part of Σ_s∈S z^s is greater than -1/2.
Let S' be the complement of S in {1,2,...,n-1).
Then for each k the real part of Σ_s'∈S' z^s' is less than -1/2.
This means that for each k there are many s'∈S' such that ks'(mod n) is close to n/2. Contradiction.

2. If n = p where p is an odd prime, then S = {1,2,...,(p-1)/2} satisfies the requirement because then (unless z = 1) Σ_s∈S z^s = -1/2 = Σ_s∈S z^-s.
In general, if n = pm where p is an odd prime, then S = {m,2m,...,m(p-1)/2} satisfies the requirement.

Problem 2019-4/C

Let n be a positive integer. Denote by S_n the permutation group on {1,2,...,n}. An element σ ∈ S_n is called representable if there exists a polynomial f ∈ Z[X] such that for all x ∈ {1,2,...,n} we have σ(x) = f(x). What is the number of representable elements of S_n?

Solution:

Suppose that σ ∈ S_n is represented by f(X) = Σ_i=0^m a_iXⁱ.
Then for all k ∈ {1,2,...,n} we have σ(k) - σ(1) = f(k) - f(1) = Σ_i=0^m a_i(kⁱ - 1), so σ(k) - σ(1) is divisible by k-1.
Since σ is a permutation on {1,2,...,n}, there are only two possibilities (dependent on the sign of a_n):
either σ(k) = k for all k and f(x) = x, or σ(k) = n+1-k for all k and f(x) = n+1-x.
(If n=1, the two solutions coincide.)

Problem 2020-1/A

For every positive integer n, we write [n] = {0,1,...,n-1}. For every integer m, we let T(m):= m (m+1)/2 be the m-th triangular number. Let τ : [n] → [n] be the map given by m → T(m) mod n.
a) For which n is τ a permutation?
b) For these n, determine the sign of τ as a function of n.

Complete solution to a) and partial solution to b):

I did some investigations with the help of a pascal program.
I found n must be a power of 2 and τ is only even for n=1 and for n=2.

a) To prove that n must be a power of 2, suppose n = n₁n₂ for odd n₁ and n₂ a power of 2.
We look for m₁ and m₂ with 0 ≤ m₁ < m₂ ≤ n-1 and τ(m₁) = τ(m₂).
If n₁ > 1 we find
m₁ = (2n₂ - n₁ - 1 )/2, m₂ = (2n₂ + n₁ - 1 )/2 if 2n₂ ≥ n₁ + 1, and
m₁ = (-2n₂ + n₁ - 1 )/2, m₂ = (2n₂ + n₁ - 1 )/2 if 2n₂ ≤ n₁ - 1,
so τ is no permutation.
If n₁ = 1, such m₁ and m₂ don't exist, so τ is a permutation.

b) As for the parity of the permutations with n = 2^k, we know that T(m) is congruent modulo 2^k to T(2^k+1-1-m).
Hence we can prove with induction that the parity is odd for k ≥ 2.

Problem 2020-1/B

Let G be a finite group of order n and R the set of the real numbers.
A map f: G → R is called a near-homomorphism if for all x, y ∈ G, we have |f(xy) - f(x) - f(y)| ≤ 1.
a) Show that for every near-homomorphism f from G to R, we have diam(f[G]) := sup_{x,y ∈ G} |f(x) - f(y)| ≤ 2 - 2/n.
b) Show that if G is cyclic, then there exists a near-homomorphism f: G → R with diam(f[G]) = 2 - 2/n.

Partial solution to a) and complete solution to b):

a) Let G = {x₁, x₂, ... , x_n} with f(x₁) ≤ f(x₂) ≤ ... ≤ f(x_n), so the diameter is f(x_n) - f(x₁).
For any x∈G we have Σ f(x_i) = Σ f(x_ix) = Σ (f(x_i) + f(x) + δ_i) = Σ f(x_i) + nf(x) + Σ δ_i with -1 ≤ δ_i ≤ 1, so f(x) = -Σδ_i/n ∈ [-1,1].
So -1 ≤ f(x₁) ≤ f(x_n) ≤ 1.
I think diam(f[G]) is maximal if G is cyclic and f as follows in b):

b) Let G be cyclic with generator g.
Then f with f(g^k) := (2k - n)/n for k ∈ {0,1,..,n-1} satisfies the requirements.

Problem 2020-1/C

Let n ≥ 4 be an integer and let A be an abelian group of order 2ⁿ. Let σ be an automorphism of A such that the order of σ is a power of 2. Then the order of σ is at most 2^n-2.

Solution:

A is the direct product of the cyclic (additive) groups Z_2^m1, ... Z_2^mr with m₁ ≤ ... ≤ m_r and m₁ + ... + m_r = n.
Let id be the neutral element of the (multiplicative) automorphism group Aut(A) of A. We have to prove that σ^2n-2 = id.
This follows from a theorem of Gausz I found in the literature: Aut(Z_2ⁿ) ≅ Z₂ x Z_2^n-2.

Problem 2020-2/B

For nonnegative integers a and b let f(a,b) := (2 min(a,b), max(a,b)-min(a,b)). We call (a,b) equipotent if for some nonnegative integers x and n holds f⁽ⁿ⁾(a,b) = (x,x). Show that if a and b are positive then (a,b) is equipotent if and only if (a+b)/gcd(a,b) is a power of 2.

Solution:

First note that f(a,b) = f(b,a), and we write (a,b) iff a ≥ b.

Now we calculate the n-th predecessor (a,b) of (x,x) for any positive x and n, that is f⁽ⁿ⁾(a,b) = (x,x). It will turn out we can do this as long as x is divisible by 2^n-1.
Predecessor 0 is (x,x) itself, and then (a+b)/gcd(a,b) = (x+x)/x = 2 is a power of 2.
Predecessor 1 is (u₁,v₁) := (3x,x), and then (a+b)/gcd(a,b) = (3x+x)/x = 4 is a power of 2.
Predecessor 2 is (u₂,v₂) := (5y,3y) with x = 2y, and then (a+b)/gcd(a,b) = (5y+3y)/y = 8 is a power of 2.
Predecessor 3 is (u₃,v₃) := (11z,5z) with x = 2y = 4z, and then (a+b)/gcd(a,b) = (11z+5z)/z = 16 is a power of 2.
Predecessor 4 is (u₄,v₄) := (21k,11k) with x = 2y = 4z = 8k, and then (a+b)/gcd(a,b) = (21k+11k)/k = 32 is a power of 2.
Predecessor 5 is (u₅,v₅) := (43m,21m) with x = 2y = 4z = 8k = 16m, and then (a+b)/gcd(a,b) = (43m+21m)/m = 64 is a power of 2.
Etc. We easily find with induction:
Predecessor n is (u_n,v_n) := ((2ⁿ⁺¹-s) x/2^n-1, s x/2^n-1) where s = u_n-1 2^n-2/x. Then (a+b)/gcd(a,b) = 2ⁿ⁺¹ is a power of 2.

On the other hand, if (a+b)/gcd(a,b) = 2ⁿ⁺¹, then we can find x,s such that (a,b) = ((2ⁿ⁺¹-s) x/2^n-1, s x/2^n-1) and then the n-th successor of (a,b) is (x,x).
Indeed, x := gcd(a,b) 2^n-1, s := b/gcd(a,b).

Problem 2020-2/C (*)

Uncle Donald cuts a 3 kg piece of cheese in an arbitrary, finite number n of pieces of arbitrary weights. He distributes them uniformly randomly among his nephews Kwik, Kwek, and Kwak. Prove or disprove: the probability that two of the nephews each get strictly more than 1 kg is at most two thirds.

Numerical solution:

For n=1 the probability is 0.
For n=2 the probability would be 1/3 if uncle Donald could choose all weights x and 3-x with x ∈ [0,3]. Indeed, if and only if he chooses an x ∈ (1,2), two of the nephews each get more than 1 kg (since both x and 3-x are greater than 1), and one gets nothing.
However, in reality only a finite number of x can occur, due to the limited capacities of uncle Donald's brain, eyes and hands. (I'm using my electronic calculator as a model of uncle Donald's brain.) But then these possible x, including x=1 and x=2, have a positive chance to be chosen, so the probability for n=2 is less than 1/3.
For n=3, the nephews may mould their cheese into three cords of equal diameter whose lengths add up to 3 units. So uncle Donald could as well have cut a cord of length 3 at two random points x and y with 0 ≤ x ≤ y ≤ 3 and distributed the three pieces with lengths x, y-x, 3-y among his nephews.
Now if Donald could choose all pairs (x,y) then the probability that two of the lengths are greater than 1 is 1/3 (see the picture below).
In reality, he can choose only a finite number of pairs (x,y). These pairs have a positive chance to be chosen, so the probability for n=3 is less than 1/3.

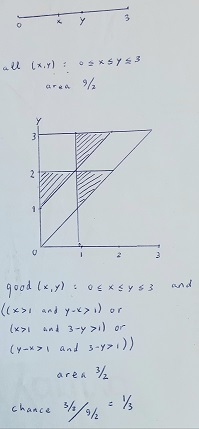
I wrote a pascal program simulating Donald's action with n pieces for 1 ≤ n ≤ 3000.
The program includes a procedure that generates n random positive numbers that add up to 3, with the help of the well known subroutine bubblesort:

program duckbrain;
var j,k,m,n,p,q,max:integer; som,t,gok,kwik,kwek,kwak:real; hulp,stuk:array[0..3000] of real;
begin
max:=0; som:=0;
for n:=1 to 3000 do
  begin
  m:=0;
  for k:=1 to 100 do
    begin
      for j:=1 to n-1 do hulp[j]:=random;
      for p:=n-1 downto 2 do
        for q:=1 to p-1 do
          if hulp[q]>hulp[p] then
            begin t:=hulp[p]; hulp[p]:=hulp[q]; hulp[q]:=t end;
      hulp[0]:=0; hulp[n]:=1;
      for j:=1 to n do stuk[j]:=3*(hulp[j]-hulp[j-1]);
      kwik:=0;kwek:=0;kwak:=0;
      for j:=1 to n do
        begin
          gok:=random;
          if gok<1/3 then kwik:=kwik+stuk[j] else if gok<2/3 then kwek:=kwek+stuk[j] else kwak:=kwak+stuk[j]
        end;
      if ((kwik>1) and (kwek>1)) then m:=m+1;
      if ((kwik>1) and (kwak>1)) then m:=m+1;
      if ((kwek>1) and (kwak>1)) then m:=m+1
    end;
    if m>max then max:=m; som:=som+m;
    writeln(n:4,m/100:13:2);
  end;
writeln('maximum ',max/100:13:2,' gemiddelde: ',som/300000:13:6); readln
end.

The output shows that the probability, as a function of n, fluctuates about a parabola with maximum 0.66 for n = 1636.
The average probability for 1 ≤ n ≤ 3000 is 0.48937 .
These results support my conclusion that the probability asked for is less than 2/3.

I tried to generalize:
Suppose uncle Donald would cut A kg of cheese in n pieces and divide them randomly among A nephews, what is the maximum probability that A-1 nephews each get more than 1 kg and for which n is this maximum attained?
I ran a modified program and found the following output:
A=4, max 0.29, n=956
A=5, max 0.13, n=549
A=6, max 0.05, n=691
A=7, max 0.02, n=192
A=8, max 0.01, n=118.

Problem 2021-2/A

A hot frying pan contains 2²⁰²¹ potato slices. Each time we toss the slices, each slice has a chance of 0.5 to land on its other side. These probabilities are individually independent. How often do we need to toss the slices so that with probability at least 0.5 all slices will have lain on both sides?

Solution:

Suppose n is the answer. Then, since for each slice the chance to land on the same side all n times is (1/2)ⁿ, we must have
(1-(1/2)ⁿ)²²⁰²¹ ≥ 0.5 and (1-(1/2)^n-1)²²⁰²¹ < 0.5.
Now since (1-1/t)^t → 1/e for t → ∞, (1-1/t)^t will for large t be close to 1/e.
This also holds for t = 2²⁰²¹ and for t = 2²⁰²², so we find that (1-(1/2)²⁰²¹)²²⁰²¹ and (1-(1/2)²⁰²²)²²⁰²² both are close to 1/e, which is smaller than 0.5.
Then (1-(1/2)²⁰²²)²²⁰²¹= (1-(1/2)²⁰²²)^22022-1 = (1-(1/2)²⁰²²)^220222-1 is close to (1/e)^2-1 = 1/√e, which is greater than 0.5.
So n=2022 is the answer.

Problem 2021-3/A

Write T = (Z/8Z)² for the torus chessboard. For every square t ∈ T its neighbours are the squares in the set {t+d/d∈D} for D = {-1,0,1}²\{(0,0)}. A line is a set of squares of the form {t+nd/n∈Z} for t∈T and d∈D.
Disprove or give an example of the following assertion: There exists a pairing of neighbouring squares, i.e. a partitioning of T into pairs {s,t} of two neighbours, such that every line contains a pair.

Partial solution:

There are 64 squares on the board. There are 32 lines: 8 running to the east (or west), 8 to the north-east (or south-west), 8 to the north (or south), 8 to the north-west (or south-east). Notice that a line may continue at an other side of the board, and neighbouring squares may sit at distinct sides of the board.
First we paint all 64 squares white. Then we choose on each of the 32 lines a pair of two neighbours, and paint them black. If these 32 chosen pairs cover T, so all 64 squares are black now, we have found a pairing as required (if we wrote down all relevant coordinates).
I wrote a program which simulates this procedure as often as we want. After ten hours of running, it gave no pairing as required as yet. Perhaps we'd better try and prove there is no such pairing.
The listing of the program is as follows:

program board;
var m,n,t1,t2,t3,t4,p,q,r,s,u,v:integer; a:array[0..7,0..7] of 0..1; partitie:boolean;
begin
  while true do
  begin
    for m:=0 to 7 do for n:=0 to 7 do a[m,n]:=0;
    for t1:=0 to 7 do begin p:=random(8); u:=t1; v:=p; a[u,v]:=1; a[u,(v+1) mod 8]:=1; write(u:2,v:2,'*') end; writeln;
    for t2:=0 to 7 do begin q:=random(8); u:=q; v:=t2; a[u,v]:=1; a[(u+1) mod 8,v]:=1; write(u:2,v:2,'*') end; writeln;
    for t3:=0 to 7 do begin r:=random(8); u:=(t3+r) mod 8; v:=r mod 8; a[u,v]:=1; a[(u+1) mod 8,(v+1) mod 8]:=1;
      write(u:2,v:2,'*') end; writeln;
    for t4:=0 to 7 do begin s:=random(8); u:=(t4+8-s) mod 8; v:=s mod 8; a[u,v]:=1; a[(u+7) mod 8,(v+1) mod 8]:=1;
      write(u:2,v:2,'*') end; writeln; writeln;
    partitie:=true;
    for m:=0 to 7 do for n:=0 to 7 do if a[m,n]=0 then partitie:=false;
    if partitie then begin writeln('gevonden!'); readln end
  end
end.

We may also try and paint on each of the 32 lines a pair of neighbour squares with one of four colors, dependent on the direction.

Problem 2021-3/B

Write φ for the Euler totient function. Determine all infinite sequences {a_n} of positive integers satisfying a_n = φ(a_n+1) for all n.

Partial solution:

An example of a solution is 1,1,1,1,2,4,8,16,32,...

Problem 2023-1/A

Does there exist a partition X of R into infinite subsets S such that, whenever for each S in the partition we choose an element c(S) of S, the set of chosen elements c(S) is dense in R?

Solution:

Yes.
Let Q be the set of the rational numbers in R.
Let ~ be the equivalence relation in R defined by r ~ r' iff r - r' is an element of Q.
Let X be the partition of R into the equivalence classes S of ~.
For each S in X, choose any representative c(S) = r in S.
Then S = r + Q.
Now imagine we draw all horizontal lines y = q with q in Q, and all vertical lines x = r where r is a chosen element c(S) in R, with intersection points that we label r + q.
Since the set of horizontal lines y = q is countable and the set of intersection points r + q is uncountable, the set of vertical lines x = r is uncountable.
Therefore, since the horizontal lines y = q are dense in the x,y-plane, the vertical lines x = r are even denser in the x,y-plane. So the set of chosen elements r is dense in R.

HOME