Nederlandse Wiskunde Olympiad 2021
3) In driehoek ABC geldt is hoek ACB gelijk aan 90 graden. Het punt M is het midden van lijnstuk AB.
De lijn door M evenwijdig aan BC snijdt AC in het punt D. Het punt E is het midden van CD. Er geldt dat BD de
lijn CM loodrecht snijdt.
(a) Bewijs dat driehoeken CME en ABD gelijkvormig zijn.
(b) Bewijs dat EM loodrecht op AB staat.
Oplossing:
Geef coördinaten M(0,0), A(-1,0), B(1,0), C(cos(t), sin(t)). Dan volgt D(cos(t)/2 - 1/2, sin(t)/2) en
E(3 cos(t)/4 - 1/4, 3 sin(t)/4).
Omdat BD loodrecht staat op MC is cos(t) = 1/3.
Dus we vinden C(1/3,2√2/3), D(-1/3,√2/3), E(0,√2/2).
Dan staat ME loodrecht op AB en CM/AB = CE/AD = ME/BD = 1/2.
Benelux Mathematical Olympiad 2017
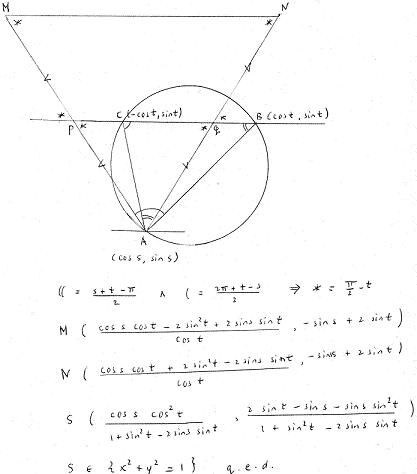
3) In the convex quadrilateral ABCD we have ∠B = ∠C and ∠D = 90 degrees. Suppose that |AB| = 2|CD|. Prove that the angle bisector of ∠ACB is perpendicular to CD.
Solution:
Consider the following picture:

Give coordinates D(0,0), C(1,0), B(1 + r cos(t), r sin(t)), A(0,a) = A(1 + r cos(t) + 2 cos(2t), r sin(t) + 2 sin(2t)).
So we can express r and a in t and verify that AC has direction vectors (-1,a) and (-cos(t), sin(t)).
Hence the vertical line through C is the angle bisector of ∠ACB.
Benelux Mathematical Olympiad 2015
4) Let n be a positive integer. For each partition of the set {1, 2, . . . , 3n} into arithmetic progressions (with at least three terms), we consider the sum S of the respective common differences of these arithmetic progressions. What is the maximal value that S can attain?
Solution:
S is maximal if the partition is {1,n+1,2n+1}, {2,n+2,2n+2}, ... , {n,2n,3n}.
So the maximal value of S is n2.
International Mathematical Olympiad 2020
6)
Prove that there exists a positive real c such that holds:
Given an integer n > 1 and a set S of n points in the plane such that each point of S is at distance at least 1
from each other point of S, there exists a straight line L that divides S such that the distance from each point of
S to L is at least c*n-1/3.
(A line L divides a set S of points if there exists a line segment between two points of S that intersects L.)
First approach:
For n=2 we must have 1/2 ≥ c*2-1/3. So c ≤ 2-2/3 = 0.62996 ...
For n≥3, the hardest case is when the points of S form a grid of equilateral triangles. Then there exists a straight line L that is at distance 1/4 from S, so we are finished if c ≤ 31/3/4 = 0.36056239 ...
International Mathematical Olympiad 2020
3) Suppose we have 4n stones with weights 1, 2, 3, . . . , 4n. Each stone is colored in one of n colors and there are 4
stones of each color. Prove that the stones can be placed in two piles A and B such that the following two conditions are
fulfilled:
one: the total weight of pile A is equal to the total wight of pile B,
two: each pile contains two stones of each color.
Partial solution:
I wrote a pascal program that does the job for each n ≤ 25. The program works also for 26 ≤ n ≤ 84, but then my output goes off the screen. For n ≥ 85, I get a runtime error: stack overflow.
program stenen;
var n,a,b,j,k,steen:integer; al:array[1..400] of boolean;
begin
while true do
begin
writeln('n? (at most 25)'); readln(n);
repeat
a:=0; b:=0;
for j:=1 to 4*n do al[j]:=false;
for k:=1 to n do
begin
write('kleur',k:4,' ');
repeat steen:=random(4*n)+1 until not al[steen]; write('stapel A',steen:4,' ');
a:=a+steen; al[steen]:=true;
repeat steen:=random(4*n)+1 until not al[steen]; write('stapel A',steen:4,' ');
a:=a+steen; al[steen]:=true;
repeat steen:=random(4*n)+1 until not al[steen]; write('stapel B',steen:4,' ');
b:=b+steen; al[steen]:=true;
repeat steen:=random(4*n)+1 until not al[steen]; write('stapel B',steen:4);
b:=b+steen; al[steen]:=true;
writeln
end;
writeln; writeln;
until a=b;
end
end.
International Mathematical Olympiad 2019
5) The Bank of Bath issues coins with an H on one side and a T on the other.
Harry has n of these coins arranged in a line from left to right. He repeatedly performs
the following operation: if there are exactly k > 0 coins showing H, then he turns over
the kth coin from the left; otherwise, all coins show T and he stops.
(a) Show that, for each initial configuration, Harry stops after a finite number of operations.
(b) For each initial configuration C, let L(C) be the number of operations before Harry stops.
Determine the average value of L(C) over all possible initial configurations C.
Partial solution:
I simulated and counted the operations of Harry for many random initial configurations with n ranging from 1 to 100,
using a Pascal program.
It turns out the average number of operations is n2/4 + n/4 + 1.
International Mathematical Olympiad 2019
3) A social network has 2019 users, some pairs of whom are friends.
Whenever user A is friends with user B, user B is also friends with user A.
Events of the following kind may happen repeatedly, one at a time:
Three users A, B, and C such that A is friends with both B and C,
but B and C are not friends, change their friendship statuses such that
B and C are now friends, but A is no longer friends with B, and no longer friends with C.
All other friendship statuses are unchanged.
Initially, 1010 users have 1009 friends each, and 1009 users have 1010 friends each.
Prove that there exists a sequence of such events after which each user is friends with at most one other user.
Partial solution:
I think initially the network must consist of two groups A and B such that A has 1010 members and B has 1009 members
and every member of A is friends with every member of B, whereas two members of A are never friends and two members of B
are never friends.
Now if a event of the described kind happens, the number of friendship relations becomes one less. I ran a Pascal program
to repeatedly simulate such an event at random. It begins with 1010*1009 friendship relations and ends with 505 friendships
relations.
International Mathematical Olympiad 2019
2) In triangle ABC, point A1 lies on side BC and point B1 lies on side AC.
Let P and Q be points on segments AA1 and BB1, respectively, such that PQ is parallel to AB.
Let P1 be a point on line PB1, such that B1 lies strictly between P and P1,
and the angles PP1C and BAC are equal.
Similarly, let Q1 be a point on line QA1, such that A1 lies strictly between Q and
Q1, and the angles CQ1Q and CBA are equal.
Prove that points P, Q, P1, and Q1 are concyclic.
Solution:
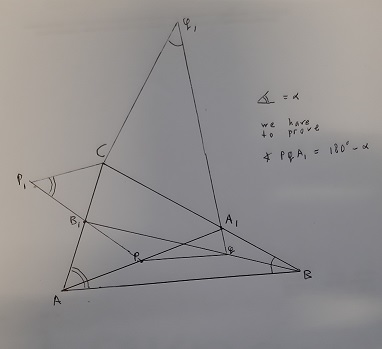
See the figure. We have to prove PA12 =
PQ2 + QA12 + 2PQ QA1 cos(α).
This is straightforward after giving coordinates as follows:
A(0,0), B(1,0), C(r cos(α), r sin(α)), A1: (1,0) + s(r cos(α) - 1, r sin(α)),
B1: t(r cos(α), r sin(α)),
P: (u + usr cos(α) -us, usr sin(α)), Q: (1 + usr cos(α) -us/t, usr sin(α)).
International Mathematical Olympiad 2018
5) Let a1 , a2 , ... be an infinite row of positive integers.
Suppose there is an integer N > 1 such that for every n ≥ N holds:
a1/a2 + a2/a3 + ... + an-1/an + an/a1
is an integer.
Prove there exists a positive integer M such that for each m ≥ M holds am=am+1.
Solution:
Suppose for each natural number M there is an m ≥ M such that am is not equal to am+1.
We have to prove that for each N > 1 there is an n ≥ N such that
a1/a2 + a2/a3 + ... + an-1/an + an/a1
is not an integer.
Let N > 1. Take M = N-1. Let m ≥ M be minimal such that am is not equal to am+1, so
for n = m+1 we have a1 = a2 = ... = an-1 and an is not equal to a1.
We have to prove that a1/an + an/a1 is not an integer.
Equivalently, let d = gcd(a1,an), a = a1/d, b = an/d, so a and b
are distinct relatively prime positive integers.
We have to prove that ab doesn't divide a2 + b2.
Since at least one of a and b must have a prime factor that doesn't divide the other, this is evident.
International Mathematical Olympiad 2017
3) A myopic but persistent hunter tries to catch a rabbit with his hands according to the following procedure:
i) They start at the same spot; the rabbit jumps to a position at distance 1 meter.
ii) As long as the hunter didn't make 1000000000 moves yet, and the rabbit is within 100 meters from the hunter,
the hunter makes a move to some spot at most 1 meter from the rabbit;
iii) After each move of the hunter, the rabbit makes a jump of 1 meter.
Can the rabbit escape from the hunter by reaching a position at least 100 meters away from the hunter within
1000000000 jumps?
Solution:
I think the best strategy of the rabbit is always jumping away from the hunter in the opposite direction, so I wrote the following Pascal program:
program imo2017-3;
const pi=3.141592654;
var a1,a2,b1,b2,t,mu,p1,p2,k,c,d:real;
begin
b1:=0;b2:=0;k:=0;a1:=0;a2:=1;
repeat
k:=k+1;
t:=random*2*pi;mu:=random;
p1:=a1+mu*cos(t);p2:=a2+mu*sin(t);
c:=sqrt((p1-b1)*(p1-b1)+(p2-b2)*(p2-b2));
b1:=b1+(p1-b1)/c;b2:=b2+(p2-b2)/c;
d:=sqrt((b1-a1)*(b1-a1)+(b2-a2)*(b2-a2));
a1:=a1-(b1-a1)/d;a2:=a2-(b2-a2)/d;
until (k>1000000000) or (d>100);
if d>100 then writeln('rabbit wins') else writeln ('hunt undecided');
writeln(k:13:0); readln
end.
I ran the program. The rabbit escaped after 4058428 jumps.
However, it's more realistic to assume the probability density f of the distance between the rabbit and the spot the hunter
runs to is not constant with f(0) = f(1) = 1, but linear and descending with f(0) = 2 and f(1) = 0.
In this case we have to use, instead of mu:=random, mu:=1-sqrt(random).
I ran the adapted program and found the rabbit escaped after 8115418 jumps.
International Mathematical Olympiad 2014
1) Let a0 , a1 , a2 , ... be a strictly increasing sequence of positive integers.
Prove there exists a unique positive integer n such that (a0 + a1 + ... + an )/n is greater than an but at most as great as an+1 .
Solution:
For each positive integer k, let tk := (ak - a0 ) + (ak - a1 ) + (ak - ak-1 ).
We have to prove there exists a unique n such that tn is smaller than an , but tn+1 is greater than an+1 .
Indeed, t1 is smaller than a1 , but, since (tk+1 - tk ) = (k+1)*(ak+1 - ak ), the sequence {tk } increases (much) faster than
the sequence {ak } , so there is a unique n where {tk } goes past {ak }.
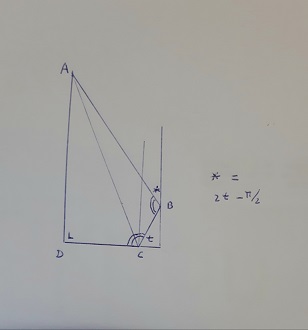
3) Let ABCD be a convex triangle with right angles at B and D. Let H on BD be such that AH is perpendicular to BD.
Let S and T be points on AB and AD, resp, such that H lies within triangle SCT and the angles CHS and CHT are 90 degrees greater than the angles CSB and CTD, resp.
Prove that the circumscribed circle of triangle STH is tangent to BD.
Partial solution:
The situation depicted in the picture amounts to a system of 25 linear equations in 24 unknown real numbers :
4 equations say the angles ABC, ADC, AHB, AHD are right, 4 others say the angles ASB, ATD, BHD are straight, 17 others say the sum of the angles in any of the 17 triangles is 180 degrees.
We want to prove that these 25 equations together with the premises e+d-u = 90 = b+c-v imply j-a = w-f , which is equivalent to the existence of M on AH such that MH = MS = MT.
I solved the system of 27 equations by expressing 18 of the variables in the other 6 (p,a,m,k,e,x), but I still need an extra equation which must yield m = e+x-90.
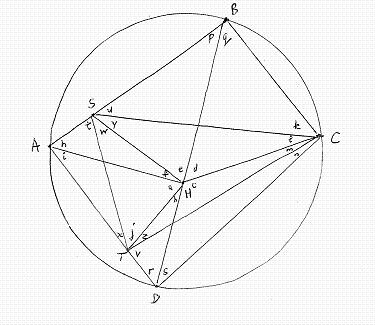
4) The points P and Q are lying on the side BC of the acute angled triangle ABC so that the angles PAB and BCA are equal, and likewise the angles CAQ and ABC.
The points M and N are lying on the straight lines AP and AQ, respectively, so that P is the center of segment AM and Q the center of segment AN.
Prove that the intersection point of the straight lines BM and CN is lying on the circumscribed circle of the triangle ABC.
Solution:
International Mathematical Olympiad 2013
4) Let ΔABC be an acute-angled triangle with orthocenter H. Let W be a point distinct from B and C on the segment BC.
Let ω1 be the circumscribed circle of ΔBWH and let X be the point on ω1 such that WX is a diameter of ω1.
Analogously, let ω2 be the circumscribed circle of ΔCWH and let Y be the point on ω2 such that WY is a diameter of ω2.
Prove that X,Y,H are collinear.
Solution:
Give coordinates H(0,0), A(-a,-1), B(b,-1), C(0,ab-1) with a,b positive and ab greater than 1. We have W(b-tb,tab-1) for some positive t smaller than 1.
Let M be the center of ω1. We find M((ab2-2b+tb+ta2b-a)/(2ab-2),(ta2b2-2ab+tb2+1-b2)/(2ab-2)) and X((ta2b+tab2-a-b)/(ab-1),(tb2+tab-ab-b2)/(ab-1)).
Let N be the center of ω2. We find N((a+b-tb-ta2b)/2,(ab-1)/2) and Y(a-ta2b,ab-tab).
We see X,Y,H are lying on the line y = mx with m = (b(1-t)/(1-tab)).
International Mathematical Olympiad 2011
1) For any set A of four distinct positive integers a1,a2,a3,a4 let sA be the sum of the elements of A and nA the number of pairs {ai,aj} of its elements such that ai + aj divides sA. Determine the sets A such that nA is maximal.
Solution:
Without loss of generality we assume a1 < a2 < a3 < a4.
nA is maximal iff ((a1+a2 divides a3+a4) and (a1+a3 divides a2+a4) and (a1+a4 divides a2+a3)) and (a2+a3 divides a1+a4)), so iff ((a1+a2 divides a3+a4) and (a1+a3 divides a2+a4) and (a1+a4 = a2+a3)).
So the elements of A are (in increasing order) a,b,c,b+c-a, where for some positive integers m,n we must have 2c+b-a = (1+m)(a+b) and 2b+c-a = (1+n)(a+c) and m is greater than n.
When we procede to express b and c in a, we get, somewhere in the middle of the calculations: (4-mn)c = (mn+4m+4)a.
So mn can only be 2 or 3, so ((m=2 and n=1) or ((m=3 and n=1)).
After completing the calculations we get A={a,5a,7a,11a} or A={a,11a,19a,29a}.
4) Let n be a natural number. We have a balance and n weights with masses 2i, i=0,..,n-1. We want to lay all weights successively on the balance, either at the left side or at the right side, in such a way that the right side is never heavier than the left side. In how many ways can we do this?
Solution:
The total number of laying all weights on the balance is n!*2n. We have to determine the fraction of layings that go wrong.
Since 2k is greater than SUM(0≤i≤k-1: 2i) for all k, the laying goes wrong iff we place a weight at the right side that is heavier than all weights laid previously.
I wrote a program to approximate the fraction f of layings that go wrong for n=1,..,100.
Among the output: for n=1 we have f=0.5, for n=2 we have f=0.375, for n=5 we have f=0.247.., for n=10 we have f= 0.177...,
for n=30 we have f=0.10.., for n=80 we have f=0.06.., for n=100 we have f=0.05...
The program:
program weegschaal;
var m,n,k,max,keus:0..100; aantal,aantalgoed:real;
gehad:array[1..100] of boolean; fout:boolean;
begin
readln(n);
aantal:=0; aantalgoed:=0;
while true do
begin
aantal:=aantal+1;
for m:=1 to n do gehad[m]:=false;
k:=0; max:=0; fout:=false;
repeat
k:=k+1;
repeat keus:=random(n)+1 until (not gehad[keus]);
gehad[keus]:=true;
if random>0.5 then if keus>max then fout:=true;
if keus>max then max:=keus
until (fout or (k=n));
if not fout then aantalgoed:=aantalgoed+1;
writeln(aantalgoed/aantal:13:10)
end
end.
Studying the output, I found the solution as follows:
The probability that with placing the k-th weight the laying goes wrong is 1/(2k). (This is the probability that the k-th weight is the maximum up to now and we place it to the right.)
So the fraction of layings that do not go wrong is PRODUCT(1≤k≤n: 1-1/(2k)).
So the number of correct layings is (2n-1)(2n-3)(2n-5)...5.3.1.
International Mathematical Olympiad 2001 (Allegedly, no solution has been published up to now.)
5) Let ABC be a triangle and let the angle at A be 60 degrees. Let X belong to BC such that AX bisects the angle at A. Let Y belong to AC such that BY bisects the angle at B. Suppose AX+BX = AY+BY. Determine the possible values in degrees of the angle β at B.
Solution:
The possible values are β=60 and β=30 only. This can be proved as follows:
Give coordinates A(0,0), B(c,0), C(1/2,√3/2) = C(c-ρcos(β),ρsin(β)), X(τ(√3/2,1/2)) = X(c-σcos(β),σsin(β)),
Y(ζ(1/2,√3/2) = Y(c-ωcos(β/2),ωsin(β/2)).
From AX+BX = AY+BY we have σ+τ = ζ+ω.
Now we can express c,ρ,σ,τ,ω,ζ in β. Subsequently, using σ+τ = ζ+ω we get:
(2sin(β)+1)(sin(β/2)+√3cos(β/2)) = (2sin(β/2)+√3)(cos(β)+√3sin(β)).
Let p:=sin(β/2). We use the wellknown goniometrical formulas and take squares to eliminate roots. Then we get a polynomial equation in p of degree six.
Since p=0 and p=1/2 (corresponding to β=60) clearly are solutions, we can divide by p and 2p-1. Thereafter we have:
(64-32√3)p4 + (-16+16√3)p3 + (-80+48√3)p2 + (20-12√3)p + (24-14√3) = 0.
After a numerical exploration up to 10 decimal places we guess this equation has no other solution than the one corresponding to β=30 and (hence) p=(√6-√2)/4.
For this value of p the left hand side is exactly zero.
Analysis of the derivatives shows that there are no other zeros of the left hand side between 0 and 1.
International Mathematical Olympiad 1997 (generalized problem)
5) For natural numbers s and t find natural numbers a and b such that abs = bat.
Solution:
Of course, a=b=1 yields a solution, and if s=t then a=b. Henceforth we only observe non-trivial solutions.
Then from unique prime factorization we deduce there must be natural numbers n, a1, ... , an, b1, ... , bn, and primes p1, ... , pn,
such that
a = p1a1 ... pnan, b = p1b1 ... pnbn
and aibs = biat for all i ∈ {1,..,n}.
So there must exist natural numbers f and g with gcd(f,g)=1 such that fai = gbi, and natural numbers ci := bi/f = ai/g.
For c := p1c1 ... pncn we have a = cg, b = cf and
g/f = ai/bi = at/bs = cgt/cfs, so fcgt = gcfs.
Now for given s and t we readily find the solutions.
For instance, if s=2 and t=1 we have fcg = gc2f. Then we consider three cases:
If g < 2f then f/g = c2f-g, g=1, f = c2f-1. If c=1 we get trivial solutions, else f ≥ 22f-1, yielding a contradiction.
If g = 2f then from fcg = gc2f we find g=f, yielding a contradiction.
If g > 2f then g/f = cg-2f, f=1, g = cg-2, so either g=3, c=3, b=3, a=27, or g=4, c=2, b=2, a=16.
Another example: s=3 and t=2, so fc2g = gc3f.
As above we find one nontrivial case with g = c2g-3 and f=1, g=2, c=2, b=2, a=4.