uitwerkingen (gedeeltelijk)

100)
i) rechten door 0.
ii) x_u = (1, v, v²) en x_v = (0, u, 2uv) zijn afhankelijk als u=0. Dit punt is echt singulier.
iii) De normaal is evenredig met x_u ⊗ x_v, en dus met (v², -2v, 1). Raakvlak v²x₁ - 2v x₂ + x₃ = 0.
iv) De vergelijking van het raakvlak is onafhankelijk van u.

110) De eerste fundamentaalvorm is hier 5(du)² + u²(dv)², dus a_{1 1} = 5, a_{1 2} = 0, a_{2 2} = u².
Uit cos(φ) = (Σ a_{i j} da_i db_j)/(√(Σ a_{i j} da_i da_j)√(Σ a_{i j} db_i db_j)) met a₁ = b₂ = t² en a₂ = b₁ = t³, volgt, als t=1, cos(φ) = 36/(7√29).

111) x_u = (1,2u,v) en x_v = (1,2v,u), dus a_{1 2} = 0 als uv = -1/5, dus x = (v - 1/(5v), v² + 1/(25v²), -1/5), dus y - x² = 2/5 en z = -1/5.

112) (ds)² = (dθ)² + sin²(θ) (dφ)².
Het oppervlakte-element is dus √ sin²(θ) dθ dφ.
De gevraagde oppervlakte is dan ₀ ∫ ^2π _θ2 ∫ ^θ1 sin(θ) dθ dφ = 2π (cos(θ2) - cos(θ1)).

113) Parametriseer het platte vlak als volgt: (u√2) (cos(v/√2), sin(v/√2), 0). Dan hebben beide oppervlakken eerste fundamentaalvorm 2(du)² + u² (dv)².

117) Met φ(u,v) = u vinden we φ_u = 1, φ_v = 0 ; dus de differentiaalvergelijking wordt:
du/dv = (a_{2 2}φ_u - a_{1 2}φ_v)/(a_{1 1}φ_v - a_{1 2}φ_u) = -a_{2 2}/a_{1 2} = -(2+u²)/(uv).
Er komt u du/(2+u²) = -dv/v, dus ln(2+u²) = -2 ln |v| + c. Hieruit volgt v²(2+u²) = μ.

118) De meridianen worden gegeven door φ(θ,φ) = λ, met φ(θ,φ) = φ, dus door φ = λ.
Er komt φ_θ = 0 en φ_φ = 1, dus de differentiaalvergelijking wordt cos(α) = (-a_{1 1}dθ - a_{1 2}dφ)/(√a_{1 1}*√(a_{1 1}dθ² + 2 a_{1 2}dθ dφ + a_{2 2}dφ²).
Met a_{1 1} = 1, a_{1 2} = 0 en a_{2 2} = sin²(θ) komt er cos(α) = -dθ / √(dθ² + sin²(θ) dφ²), dus dθ/sin(θ) = +tg(α) dφ.
Dan volgt voor de loxodromen: φ + c = + (1/2) cotg(α) ln(|(1+cos(θ))/(1-cos(θ))|).

127) f ' = 0, dus f constant; we hebben dan een recht schroefoppervlak. Of h=0, omwentelingsoppervlak.

128) (ds)² = (du)² + (u²+h²) (dv)² , dus a_{1 1} = 1, a_{1 2} = 0, a_{2 2} = u²+h².
φ(u,v) = u, zodat φ_u=1, φ_v=0. Er komt in 116:
(1/2)√2 = (u²+h²) dv / (√(u²+h²) √((du)² + (u²+h²)(dv)²)), dus: +du/√(u²+h²) = dv.
Hieruit volgt: ln | u + √(u²+h²) | = +v + c.

129) De parameterlijnen snijden elkaar loodrecht in punten waar uv = b²-a².

130) Zij x(u₁(t),u₂(t)) zo'n bissectrix.
Door gelijkstellen van de hoek met de u₁-lijn aan de hoek met de u₂-lijn vindt men via 116 (met φ(u₁,u₂) = u₁ en φ(u₁,u₂) = u₂ respectievelijk):
(a_{1 2} du₁ + a_{2 2} du₂)/√a_{2 2} = +(a_{1 1} du₁ + a_{1 2} du₂)/√a_{1 1}.
Hieruit volgt (mits a_{1 2}² - a_{1 1} a_{2 2} ≠ 0) : a_{1 1} (du)² = a_{2 2} (dv)².

131) Pas 120 toe.

137) De parameterlijnen vormen een orthogonaal net omdat a_{1 2} = 0.
De indicatrixvergelijking luidt du dv = 1 (mits b ≠ 0), omdat h_{1 1} = h_{2 2} = 0 en h_{1 2} = -b/√(b²+(a+u)²) (reken na). Dit is een orthogonale hyperbool met asymptoten du = 0 en dv = 0.
Het net der asymptotische lijnen is du dv = 0, dit is het net der parameterlijnen.

145) Reken na dat a_{1 1} = 1 + (f ' )², a_{1 2} = 0, a_{2 2} = u²; h_{1 1} = f " / √(1 + (f ' )²), h_{1 2} = 0, h_{2 2} = u f ' / √(1 + (f ' )²).
Met h_{1 1}a_{2 2} - 2 h_{1 2}a_{1 2} + h_{2 2}a_{1 1} = 0 komt er f ' / (1 + (f ' )²) = -uf ".
Beschouw dit als een differentiaalvergelijking in f ' (stel f ' = g), en vind na het scheiden van de variabelen met partiële breuksplitsing (f ')² = c²/(u²-c²).
Er komt f = +c log((u + √(u²-c²)/c), ofwel u = c cosh(f/c).

De kettinglijn is de kromme gevormd door een homogeen koord onder invloed van de zwaartekracht. Zij lijkt op een parabool, maar is daarvan wezenlijk verschillend.
De vorm van de catenoïde wordt aangenomen door een zeepvlies gespannen tussen twee cirkelvormige draadfiguren waarvan de middelpunten recht boven elkaar liggen.

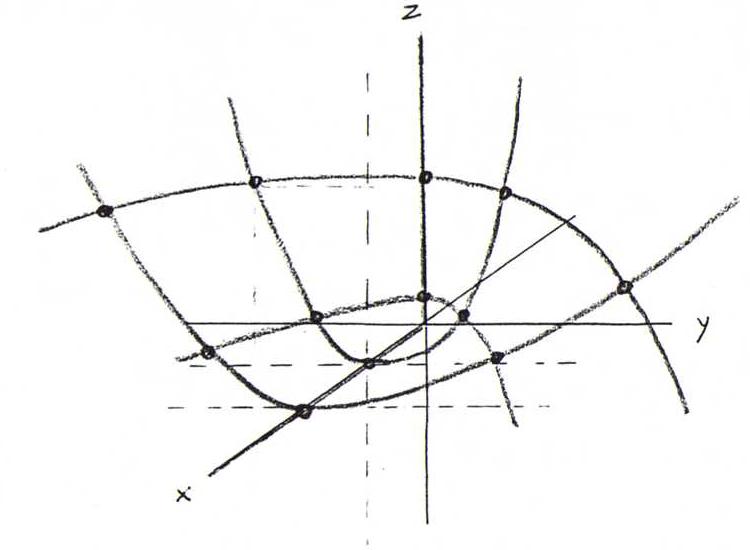
Extra opgave :

a) (zie plaatje hierboven)
u-lijnen: parabolen in vlakken z=constant, x≥0.
v-lijnen: parabolen in vlakken x=constant, z≥0.

b) Eerste fundamentaalvorm (4u²+v²)(du)² + 2uv du dv + (u²+4v²)(du)².
De parameterlijnen staan loodrecht op elkaar waar uv=0, dus op de x- en z-as.

c) Tweede fundamentaalvorm (2/√((u²+v²)²+2u²v²) (v²(du)² - 2uv du dv + u²(dv)²).
Indicatrix (2/√..) (v du - u dv)² = 1, twee evenwijdige lijnen met richtingsvector x_u + (v/u)x_v.
Asymptotische lijnen du/dv = u/v, u=cv, x = v²(c²,c,1) (halve rechte lijnen).

d) Orthogonale trajectoriën van de u-lijnen uit x_u . (x_u+ x_v dv/du) = 0.
Er komt du/dv = - (4u²+v²)/(uv) en uiteindelijk v²u² + 4u⁴ = constant.

e,f) Blijkens c) bestaat het oppervlak uit halve rechte lijnen v²(c²,c,1) = λ(t²,t,1) (λ positief). De rechten vertrekken uit (0,0,0) (top) en gaan door (t²,t,1) (richtkromme, een parabool). Het is dus een halve parabolische kegel.
Raakvlakken (vergelijking v²x - 2uv y + u²z = 0) zijn op regel u = cv constant (vergelijking x - 2cy + c²z = 0).

f) Parametrizering λ(t²,t,1): zie boven bij e).
De regels zijn de λ-lijnen, dus de orthogonale trajectoriën van de regels volgen uit x_λ . (x_λ+ x_t dt/dλ) = 0. Er komt dt/dλ = -(t⁴+t²+1)/((2t³+t)λ).
Uiteindelijk vinden we λ||(t²,t,1)|| = constant, dus een orthogonale trajectorie bestaat uit punten op vaste afstand van (0,0,0).

153) Als de meridiaankrommen van een schroefoppervlak kromtelijnen zijn, dan moet dv = 0 oplossing zijn van 148, dus a_{1 1} h_{1 2} - a_{2 1} h_{1 1} = 0.
Er volgt h (1 + (f ' )² + u f ' f " ) = 0. Dus h = 0 of f ' f " /(1 + (f ' )²) = -1/u. Dit geeft de gestelde oplossingen.

154) Reken na dat a_{1 2} = h_{1 2} = 0 en gebruik stelling 152.

155) Reken na dat a_{1 2} = h_{1 2} = 0 en gebruik stelling 152.

165) x ' = 0 geeft een kegel; e ' = 0 geeft een cylinder. Stel verder x ' , e ' ≠ 0.
Als y(u) = x(u) + v(u) e(u) nu de keerkromme is, dan is y '(u) = x '(u) + v(u) e '(u) + v '(u) e(u) evenredig met e(u) (want x ' + v e ' is evenredig met e door onze keuze van v).
Dus is het regeloppervlak een raaklijnenoppervlak.

EO) Bewijs eerst dat de singuliere punten de punten zijn met u=v, en bepaal de kandidaat-keerkromme x(t) met t:=u=v en het bijbehorende raaklijnenoppervlak x(t) + λ x '(t).
Bewijs door een coördinatentransformatie dat dit raaklijnenoppervlak samenvalt met het oorspronkelijke.

180) x = q(cos(t),sin(t),t/p) (cirkelschroeflijn) ; x = (t,t²,t³) (kubische parabool).

181) x = (t cos(t) - sin(t), t sin(t) + cos(t)) (de ontwindende van een cirkel).

189) Ga na dat de Christoffelvergelijkingen 186 hier luiden u^.. = v^.. = 0

190) Stel de differentiaalvergelijkingen 186 op. Er komt:
u(u ^.)² - u(v ^.)² + (1+u²) u ^.. = 2 u ^. v ^. + u v ^.. = 0.
Verder is (ds)² = (1+u²)(du)² + u²(dv)².
Uit de tweede Christoffelvergelijking volgt v ^. = c/u², dus
u⁴(dv)² = c²(ds)² = c²((1+u²)(du)² + u²(dv)²).
Hieruit volgt v = + ∫ (c/u) √((1+u²)/(u²-c²)) du.
Met c=0 vindt men de meridiaankrommen.

191) Ga uit van x = (u cos(v), u sin(v), a*u). We vinden:
(ds)² = (1+a²)(du)² + u²(dv)², -u (v ^.)² + (1+a²) u ^.. = 2 u ^. v ^. + u v ^.. = 0.
Als in 190 is u⁴(dv)² = c²(ds)². Hier geeft dit:
u⁴(dv)² = c²(1+a²)(du)² + u² c² (dv)², waaruit:
v = +√(1+a²) ∫ c/(u √(u²-c²)) du.
Met t = √(u²-c²) vindt men v = +√(1+a²) arctan(√(u²-c²)/c) + d.

Merk op dat de oplossingen in 190 en 191 voldoen aan het gegeven dat in elk punt in elke richting een geodeet vertrekt.

199)
a) Reken na dat de indicatrix wordt (2/√...) (du - dv)² = 1.
Elk punt is parabolisch, maar er zijn geen singuliere punten (want N is nergens 0). Het oppervlak moet dus een cylinder zijn.
Asymptotische krommen vindt men met du = dv, u = v + c, dus hun parametriseringen zijn (1+c, c, c²) + v(0, 1, 1). We hebben dus de richtkromme (1+c, c, c²) en de asrichting (0,1,1).

b) Een eenvoudigere parametrisering is (1+w, w, w²) + v(0, 1, 1).
De differentiaalvergelijkingen worden:
(2+4w²)(w ^.)² + 2(1+2w)(w ^.)(v ^.) + 2(v ^.)² = 1
((4w-2)/(4w²-4w+3))(w ^.)² + (w ^..) = 0
((4-4w)/(4w²-4w+3))(w ^.)² + (v ^..) = 0
Oplossingen zijn onder andere: w(s) = c₁, v(s) = +(1/2)√2 s + c₂ (de beschrijvenden).

200) Beide oppervlakken hebben als eerste fundamentaalvorm r² (du)² + 2 (dr)². Het eerste oppervlak is een rechte cirkelkegel, het tweede een plat vlak.

201)
a) Asymptotische lijnen uit (1/u)(du)² - (2/v)(du)(dv) + (u/v²)(dv)² = 0 = (du/u - dv/v)², dus elk punt is parabolisch.
Oplossen van du/dv = u/v geeft u = cv. Parametervoorstelling van de asymptotische lijnen v(c², c, 1/c).
b) Blijkens a) is het oppervlak parametriseerbaar als v(c², c, 1/c), dus het bestaat uit rechten door 0. Het is dan een kegel, dus het is afwikkelbaar.

203)
a) (x_u . x_v)/(||x_u||.||x_v||) = cos(α), dus a_{1 2} = cos(α) √(a_{1 1}a_{2 2}).
b) Stel x(u,v(u)) is zo'n trajectorie. Eis ((x_u) . (x_u + x_v dv/du))/(||x_u||.||x_u + x_v dv/du||) = (1/2)√3, dus (a_{1 1} + a_{1 2} dv/du)/(√a_{1 1} . √(a_{1 1} + 2 a_{1 2} dv/du + a_{2 2}(dv/du)²)) = (1/2)√3.

204)
a) De u-lijnen zijn congruent met de grafiek van g; de v-lijnen zijn rechte lijnen; U is een 'golfplaat' (cylinder met sinusoïde als richtkromme).
b) Een eenvoudigere parametrisering van U wordt gegeven door (w,u,g(u)) met eerste fundamentaalvorm (1+g'(u)²) (du)² + (dv)².
Het plat vlak z=0 wordt geparametriseerd door (w,f(u),0) met eerste fundamentaalvorm f '(u)² (du)² + (dv)².
Neem nu f zo dat f '(u) = √(1+g'(u)²).

205)
a) Beschouw twee oppervlakken x(u,v) en y(u,v).
Als twee krommen op het eerste oppervlak elkaar in een bepaald punt raken, zijn ze beeldkrommen van twee krommen in het u,v-vlak die in het origineel van het raakpunt raken aan een gemeenschappelijke raaklijn met richtingscoëfficiënt dv/du. Dus dan hebben die krommen in dat punt beide dezelfde raakrichting x_u + x_v dv/du.
Onder het diffeomorfisme yox^-1 gaan ze over in twee krommen op het tweede oppervlak die beide dezelfde raakrichting y_u + y_v dv/du hebben.
Dus raken is invariant onder alle diffeomorfismen, niet alleen onder isometrieën.
b) Als men een rechte cirkelcylinder verbuigt tot een plat vlak, gaat een cirkel over in een rechte, dus dan is de kromming niet invariant.

207)
a) Met u dv + v du = 0 vindt men een familie asymptotische lijnen op het oppervlak. Er komt uv = c, en hiermee vindt men de alternatieve parametrisering (c, c², c³) + u(c, c, c²). Bij deze parametrisering zijn de u-lijnen rechte lijnen.
b) x_u ⊗ x_c = (-c³ - uc², 3c³ + uc² - c², c - 2c²) is afhankelijk van u, dus het raakvlak is niet constant langs de regel, dus nee.
Alternatief : Met x_u ⊗ x_c = 0 vindt men twee singuliere punten, namelijk (0,0,0) en (1/4,0,0). Een cylinder heeft geen singuliere punten, een kegel heeft er één, een raaklijnenoppervlak heeft een hele kromme van singuliere punten.
c) Neem v=1 en u=t (of c=u=t).
d) De oppervlaktenormaal is evenredig met (-2t³, 4t³-t², t-2t²), de hoofdnormaal staat loodrecht op x ' ⊗ x " = (24t², -12t-12t², 4).
Als k een geodeet is, moeten N en n steeds evenredig zijn, dus (-2t³, 4t³-t², t-2t²) en (24t², -12t-12t², 4) voor alle t loodrecht op elkaar. Dit geldt bijvoorbeeld niet voor t=1. Dus k is geen geodeet.