Hoofdstuk 3: PROJECTIEVE TRANSFORMATIES VAN HET PROJECTIEVE VLAK

§ 15: Collineaties en projectieve afbeeldingen

Definitie : Een collineatie van P² is een bijectie φ van P² op zichzelf waarbij punten op punten worden afgebeeld en lijnen op lijnen, terwijl φ(A) op φ(l) ligt precies dan als A op l ligt.

Stelling : Een collineatie behoudt de harmonische ligging van puntenparen (en evenzo van lijnenparen).

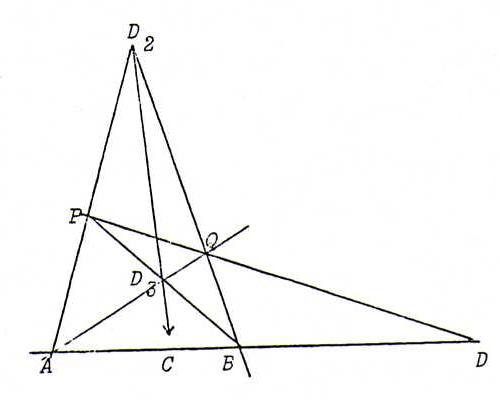
Bewijs : Stel dat {A,B} en {C,D} harmonisch scheidende paren op een puntenreeks l zijn.
Vorm een volledige vierhoek ABPQ met diagonaalpunten D = D₁ = AB.PQ, D₂ = AP.BQ, D₃ = AQ.BP.
Dan is dus C = l.D₂D₃ (zie §12).

Noteert men het beeldpunt van X onder de collineatie als X ' , dan blijkt:
vierhoek ABPQ gaat over in vierhoek A ' B ' P ' Q ' met diagonaalpunten D₁ ' , D₂ ' , D₃ ' .
Dus C ' is de vierde harmonische bij {A ' , B ' } en D ' .

Definitie : Een projectieve afbeelding van P² op P² is een collineatie van P² die de dubbelverhouding bewaart.

Opmerking : De projectieve afbeeldingen zijn precies de continue collineaties.

Fundamentele stelling : Zijn A, B, C, D vrijgelegen punten in P², en evenzo A ' , B ' , C ' , D ' , dan is er precies één projectieve transformatie van P² die A overvoert in A ' , B in B ' , C in C ' , en D in D ' .

Bewijs :

1) uniciteit : Stel φ en ψ voldoen. Dan is φψ^-1 een projectieve afbeelding met vier vrijgelegen dekpunten, dus de identiteit (zie O59). Dus φ = ψ.

2) existentie : Gebruik projectieve coördinaten. Representeer X in P² door λx met x ∈ ℜ³. Leg x vast door ||x|| = 1, x₁ + x₂ + x₃ positief.
Laat nu α, β, γ ∈ ℜ bepaald zijn door d = αa + βb + γc (αβγ≠0).
Laat ρ, σ, τ ∈ ℜ bepaald zijn door d ' = ρ(αa ' ) + σ(βb ' ) + τ(γc ' ) (ρστ≠0).
Zij P de lineaire transformatie van ℜ³ gedefinieerd door P(a) = ρa ', P(b) = σb ', P(c) = τc '.
Dan is P(d) = d ', en P induceert op P² een collineatie als gevraagd.
Zie nu O61 voor het vervolg.

Opmerking : Uit het bewijs onder 2) hierboven en O61 blijkt dat elke projectieve transformatie van P² geïnduceerd wordt door een reguliere lineaire transformatie van ℜ³ (en door elk λ-voud daarvan , λ ≠ 0).
Dit gebruikten we in §6.

Opgave 59 : Bewijs dat elke projectieve transformatie met vier vrijgelegen dekpunten de identiteit is.
Hint: ga uit van de vierhoek ABCD der dekpunten, en gebruik de stellingen van §10.

Opgave 60 : Zij φ een projectieve transformatie van P². Zij L een punt in P².
Toon aan dat φ een projectiviteit induceert van de lijnenwaaier L op de lijnenwaaier L ', met L ' = φ(L).
Toon aan dat φ de identiteit is als φ twee waaiers lijn voor lijn invariant laat. Dualiseer.

Opgave 61 : Zij P een reguliere lineaire transformatie van ℜ³.
Toon aan dat P de collineariteit van drie punten A, B, C op een lijn l bewaart, en de verhouding van lijnstukken: AB/AC = P(A)P(B)/P(A)P(C).
Laat vervolgens zien dat de door P op P² geïnduceerde collineatie φ de dubbelverhouding bewaart.

Opgave 62 : Gegeven zijn vier vrijgelegen punten A, B, C, D, en vier vrijgelegen punten A ' , B ' , C ' , D ' .
Construeeer bij een willekeurig punt X het beeldpunt onder de projectieve transformatie die A in A ' overvoert, B in B ', C in C ' , en D in D ' .
(Hint: projecteer D vanuit elk der hoekpunten van driehoek ABC op de tegenoverliggende zijde en doe hetzelfde met D ' en A ' B ' C ' . Herleid de constructie nu tot die van de op de zijden van ABC geïnduceerde projectiviteiten en gebruik Steiner.)

uitwerkingen