PROJECTIVE GEOMETRY COURSE
§ 9: Separation and cross ratio
Given four distinct points A,B,C,D on a line l.
After choosing an orientation of l, the distances have a sign such that AB = - BA, etc.
We define the cross ratio of A,B,C,D (in this order) by (A,B;C,D) = (AC/AD)/(BC/BD).
The cross ratio is independent of the orientation of l.
We say the pairs {A,B} and {C,D} separate each other if (A,B;C,D) is negative (this means that one of the points C,D
is lying between A and B, and the other is not. See O36.
Proposition : Separation and cross ratio are invariant under a perspectivity from a line onto a line.
Proof : (see O35, too)
That separation is invariant, is evident (but distinguish between the case that P is lying between l and l' and the other case). Furthermore:
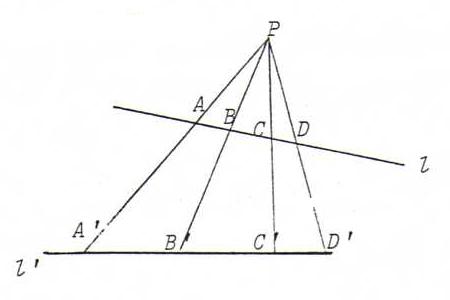
Let H be the foot point of the line through P perpendicular to l. If we forget the signs, we have:
(AC/AD)/(BC/BD) = ((AC . HP/2)/(AD . HP/2))/((BC . HP/2)/(BD . HP/2)) =
((area ΔAPC)/(area ΔAPD))/((area ΔBPC)/(area ΔBPD)) =
((AP.CP sin∠APC)/(AP.DP sin∠APD))/((BP.CP sin∠BPC)/(BP.DP sin∠BPD)) =
((sin∠APC)/(sin∠APD))/((sin∠BPC)/(sin∠BPD)) =
((sin∠A'P'C')/(sin∠A'P'D'))/((sin∠B'P'C')/(sin∠B'P'D')) = (A'C'/A'D')/(B'C'/B'D').
For four lines a,b,c,d through a point P we define the cross ratio (a,b;c,d) as
(a.l , b.l ; c.l , d.l), where l is an arbitrary line, but not going through P.
The pairs {a,b} and {c,d} separate each other if {a.l , b.l} and {c.l , d.l} separate each other.
Now you yourself can define the cross ratio of four points on the line at infinity.
The following proposition is evident;
Proposition : separation and cross ratio are invariant under projectivities.
O35 Prove the last proposition but one in the case that P and/or D are points at infinity, and in the case that l is the line at infinity.
O36 Let (X1,X2;X3,X4) = λ. Calculate
(Xσ(1),Xσ(2);Xσ(3),Xσ(4)) for each permutation σ of {1,2,3,4}.
How many distinct values do we get? (Hint: (X1,X2;X3,X4) +
(X4,X2;X3,X1) = 1.)
O37 Let X1,X2,X3,X4 be four points on a line l, and
x1,x2,x3,x4 four lines through a point L, whilst Xi and xi have the same projective
coordinates. Prove that (X1,X2;X3,X4) =
(x1,x2;x3,x4).
O38 Define the function f from a line l into the set of real numbers (plus ∞ (=-∞)) by f(X) = (X,B;C,D), where B,C,D
are three distinct fixed points on l.
Prove that f is a continuous bijection with values as in the picture below:
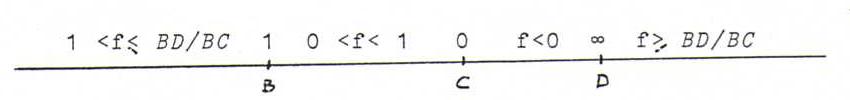
answers
HOME