PROJECTIVE GEOMETRY COURSE
§ 26: The theorem of Pascal
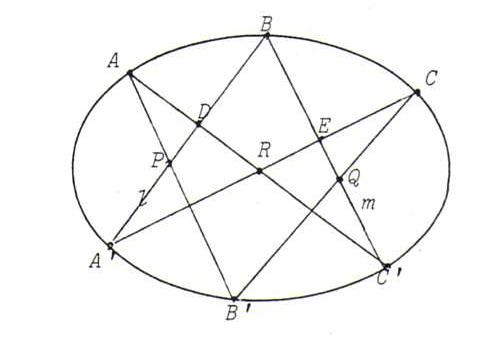
Proposition: Let A, B, C, A ', B ', C ' be points that lie on a non-degenerated conic J.
Then P := AB '. A 'B, Q := BC '. B 'C and R := AC '. A 'C are lying on one and the same line (the pascal line
of hexagon ABCA 'B 'C ').

Proof: J is the conic generated by the projectivity φ from A onto C with φ(AA ' ) = CA ', φ(AB ' ) = CB ',
φ(AB ) = CB. Since C ' lies on this conic, φ(AC ' ) = CC '.
Let D := A ' B . AC ', E := A ' C . BC ', l := A ' B, m := BC '. Then we have:
l(A ', P, D, B) ∧= A(AA ', AP, AD, AB) = A(AA ', AB ', AC ', AB)
∧_ C(CA ', CB ', CC ', CB) = C(CE, CQ, CC ', CB) ∧=
m(E, Q, C ', B), so l(A ', P, D, B) ∧_ m(E, Q, C ', B).
Apparently, B is fixed point of the projectivity ψ from l onto m with ψ(A ' ) = E, ψ(P ) = Q, ψ(D ) = C '.
According to O40, ψ is a perspectivity with center A ' E . DC ' = R. Since ψ(P) = Q, P, we see Q and R lie on one and the
same line.
Note: The proposition also holds in the case that one, two or three pairs of points coincide. The line connecting two coinciding points is the tangent in that point.
Note: Pascal proved his theorem by first proving it for a circle, and then projecting the whole configuration on an other plane.
Note: The dual theorem is called theorem of Brianchon:
Proposition: Let a, b, c, a ', b ', c ' be tangents to a non-degenerated conic J.
Then the connecting lines p := ab '. a 'b, q := bc '. b 'c and r := ac '. a 'c go through one and the same point
(the Brianchon point of hexagon abca 'b 'c '; the intersection point of two coinciding tangents is the contact point on that line).
Problems:
O95 Prove the theorem of Brianchon by dualising the proof of the theorem of Pascal.
O96 Let A, B, C and D be four distinct points of a non-degenerated conic J. Prove the intersection point of the tangents in A and B is collinear with the two diagonal points of quadrangle ABCD that don't lie on AB, without using the theory of poles and polar lines.
O97 The vertices of two point perspective triangles A1B1C1 and
A2B2C2 are lying on a conic J.
P is a point of J that doesn't coincide with one of these six points. X := PA2. B1C1,
Y := PB2. A1C1, Z := PC2. A1B1.
Prove that X, Y, Z and the center of perspectivity of the given triangles are collinear.
O98 Construct a sixth point of the conic through five freely situated points, using the theorem of Pascal. Likewise a sixth line of the conic of lines determined by five freely situated lines.
O99 Prove that the Pascal line of a hexagon whose vertices are lying on a conic J is the polar line of the Brianchon point of the corresponding hexagon of the tangents in these six points.
O100 Of a conic J four points and the tangent in one of these points are given. Construct the tangents in the other points. Also solve the dual problem.
O101 Solve the problems of §24 using the theorems of Pascal and Brianchon.