PROJECTIVE GEOMETRY COURSE
§ 25: The relation between conics of points and conics of lines
Proposition: The tangents to a conic of points form a conic of lines (and the points of contact to a conic of lines form a conic of lines).
Proof: Let l, m, n be tangents to a conic of points J, with contact points L, M, N.
Let X := l.m, Y := m.n, Z := l.n.
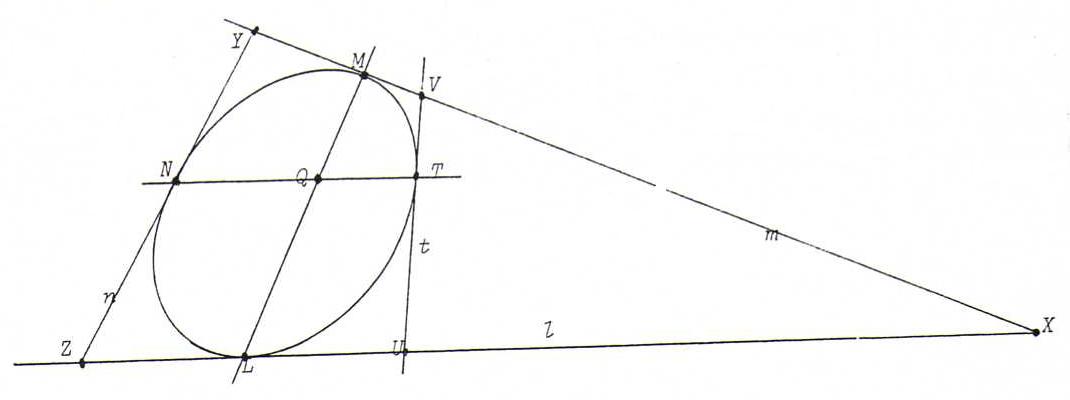
The projectivity φ : l → m with φ(X) = M, φ(L) = X and φ(Z) = Y has Pappus line p = LM.
Now let t be a fourth tangent, with contact point T.
Let U := l.t, V := m.t, Q := p.TN.
Then U and Y lie on the diagonal through Q and TM.NL of quadrangle TMNL (zie §22).
Then Y, U, Q are collinear, and likewise V, Q, Z.
According to Steiner, φ maps U to V. So t is the line connecting U and φ(U).
So each tangent to J is a line connecting a point on l and its image point under φ on m.
Problems:
O92 Suppose we have five tangents a, b, c, d, e to a conic of points J. Construct the pole of a given line x.
(Hint: if a ' is the second tangent to J through a. x, then the pole X of x lies on the fourth harmonic x ' with {a, a ' } and
x. Prove this first.)
O93 Let B and C be conjugated points with respect to a conic of points J. Suppose we have a line through C which intersects J in P and Q.
Suppose BP and BQ intersect J in two more points R and S.
Prove that C, R and S are collinear.
O94 Prove that a quadrangle ABCD with A, B, C, D on J and the quadrilateral abcd of the tangents to J in A, B, C,
D, respectively, have the same diagonal triangle.
answers
HOME
