PROJECTIVE GEOMETRY COURSE
§ 12: Harmonic separation and the complete quadrangle
Definition : Let A, B, C, D be four points on a line l. The pairs {A, B} and {C, D} separate harmonically
if (A, B; C, D} = -1.
Let a, b, c, d be four lines through a point L. The pairs {a, b} and {c, d} separate harmonically
if (a, b; c, d} = -1.
See O48.
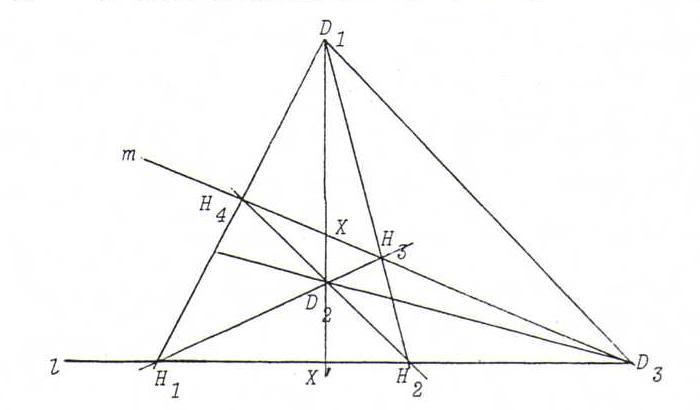
Definition : A complete quadrangle is the figure formed by four freely situated points (that is: no three collinear) and their six connecting lines (the sides).
Opposite sides are sides whose intersection points is not a vertex. We call the intersection point of two opposite sides a diagonal point. The connecting line of two diagonal
points is called diagonal.
There are three diagonal points (prove this) and three diagonals.

Proposition : If two sides and two diagonals of a complete quadrangle go through one diagonal point, they form pairs that separate harmoically.
Proof : (see the picture)
l(H1, H2, X ', D3) ∧=D2
m(H3, H4, X, D3) ∧=D1
l(H2, H1, X ', D3), so
(H1, H2; X ', D3) = (H2, H1; X ', D3).
If we call this number d, then d=1/d. So d=+1. Since the points are distinct, we get d=-1.
Remark : Strictly speaking, we don't need cross ratio to build up the projective geometry of the real projective plane. The complete quadrangle alone is already sufficient, but then we have to
formulate some axioms of order and continuity.
(See Coxeter : "The real projective plane".)
Problems:
O48 Suppose (X1, X2; X3, X4) = -1. Find all permutations σ of {1,2,3,4} such that (Xσ(1), Xσ(2); Xσ(3), Xσ(4)) = -1.
O49 Let A, B, C be three points on a line l. Use the figure of the complete quadrangle to construct the fourth harmonic with {A, B} and C (this is X such that (A, B; C, X) = -1).
O50 Let A0A1A2A3 and B0B1B2B3 be complete
quadrangles with
A2 = B2 , A3 = B3 and D1 :=
A0A1 . A2A3 =
B0B1 . B2B3 := E1.
Define the other diagonal points as follows:
D2 := A0A2 . A1A3 ,
E2 := B0B2 . B1B3 ,
D3 := A0A3 . A1A2 ,
E3 := B0B1 . B1B2 .
Prove that D2D3 , E2E3 and A2A3 concur.
O51 Let P be a point that's not lying on a side of triangle ABC. Construct the line that intersects BC, CA and AB in D, E, F respectively, in such a way that {P, F} and {D, E} separate harmonically. (See O49.)