PROJECTIVE GEOMETRY COURSE
§ 11: Line and point of Pappus
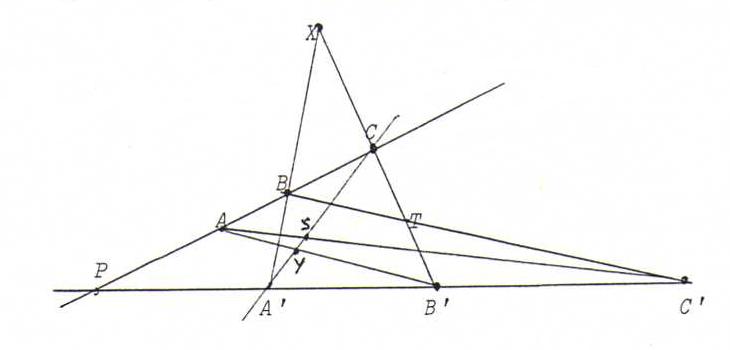
Theorem of Pappus : Let A, B, C be three points on a line l, and
A', B', C' three points on an other line m. Then the points AB'.BA', AC'.CA', BC'.CB' lie on one line (the Pappus line of the sextet).
Proof: Look at the figure beneath:

We find (B', T, C, X) ∧=B (B', C', P, A') ∧=A
(Y, S, C, A').
So the projectivity that maps B' to Y, T to S and X to A', leaves C invariant. Hence, according to O40, it is a perspectivity.
So B'Y, TS and XA' concur. This is what we had to prove.
Theorem of Steiner : Let φ be a projectivity from a line l onto an other line m. Then all points Xφ(Y).Yφ(x) with X, Y on l,
are collinear (on the Pappus line of the projectivity).
Proof: Choose three points A, B, C on l, and let A':=φ(A), B':=φ(B), C':=φ(C). Let p be the Pappus line of the sextet.
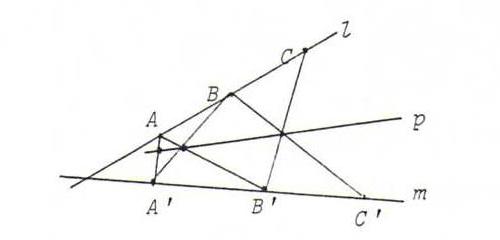
If γ is the perspectivity from l onto p with center A', and δ from p onto m with center A, then φ = δoγ (because φ and
δoγ both map A, B, C into (respectively) A', B', C' , FS).
So for X on l we find φ(X) by first projecting X from A' onto p, and, subsequently, the image point from A onto m (Steiner construction).
Hence, if X and Y are arbitrary points on l, then p is the line through XA'.Aφ(x) and YA'.Aφ(Y). Applying the theorem of Pappus on
A, X, Y, A', φ(X), φ(Y), we find that Xφ(Y).Yφ(x) lies on p.
O43 Let φ be a projectivity from a line l on an other line m. With the help of the theorem of Steiner, find the image point of p.l, and the image point of
l.m.
Show with the help of O40 that φ is a perspectivity if and only if l, m and p go through one point. Give also the dual assertion.
O44 Let φ be a projectivity from a line l onto an other line m. Suppose we know the Pappus line and a pair (A, φ(A)) of φ.
Check in which cases there is exactly one φ with these data. Give also the dual assertion.
O45 Let a, b, c be three lines through a point L and a', b', c' three lines through an other point M.
Let φ be the projectivity from L onto M with φ(a) = a ', φ(b) = b ', φ(c) = c '.
Construct thet Pappus point of the projectivity.
Let l be a fourth line through L. Construct φ(l).
O46 Look at the following figure and study the text under it. Subsequently, prove the theorem of Desargues.
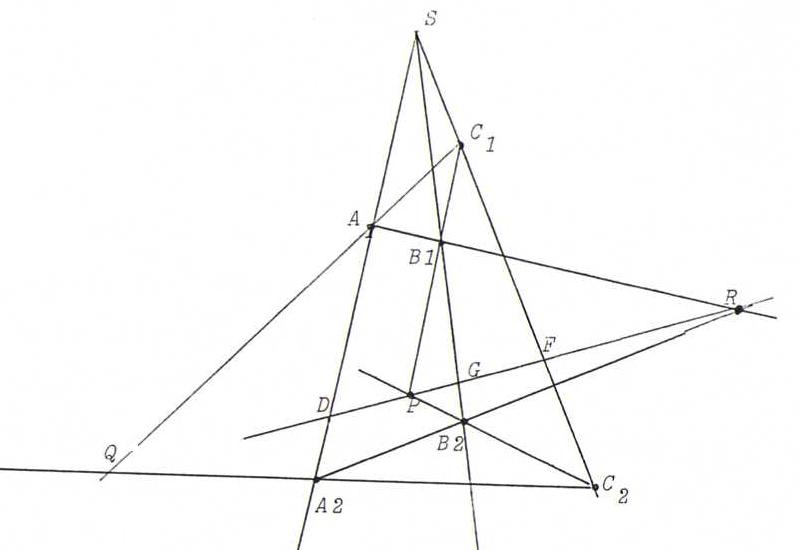
The triangles A1B1C1 and A2B2C2 are perspective from S.
So we have to show that PR goes through Q.
So we seek a projectivity with (S, A1, D, A2) ∧- (S, C1, F, C2).
Then this is a perspectivity because of O40, and we find what we had to prove.
O47 In the situation of O34, construct for arbitrary X on l the image point X ' with the help of Steiner.