§ 4: answers

O12 The line at infinity in α corresponds under the rotation to the line at infinity in β (indeed, a bundle of parallel lines is mapped onto a bundle of parallel lines).
The line at infinity in β is projected onto u (a bundle of parallel lines in β is mapped onto a bundle through a point of u).
Under the central projection, the line at infinity of α corresponds to s. So the original is s", that is the line in α with which s coincides after rotating β onto α (we have to agree upon a direction of rotating).

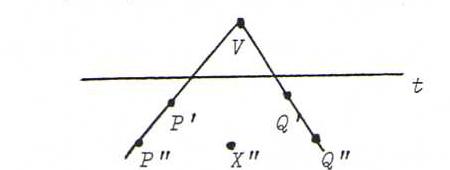
O13 Choose a point P" with image P' (unequal to P") and a point Q", not on P"P', with image Q' (unequal to Q"). Let V be the point of intersection P"P'.Q"Q'.
Now let X" be a point, not V, not on t or P"P' or Q"Q'.

Since a line and its image intersect on t, the triangles P"Q"X" and P'Q'X' are line perspective from t. So they are correspondingly point perspective. So X"X' goes through V.
Next, continue with X" on P"P', etcetera.

O14

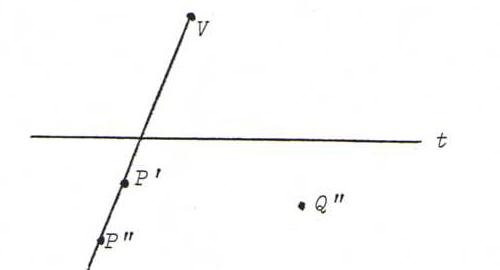
Q' lies on VQ", but also on P'S where S = t.P"Q".

O15

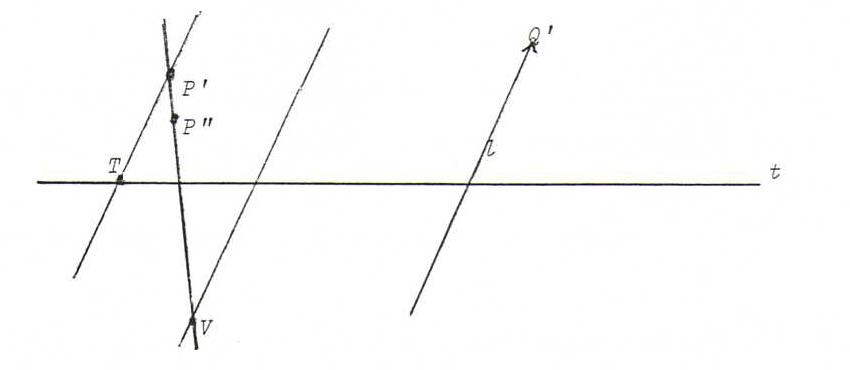
The construction is the same as in O14.
Start with a line l, unequal to t or P'P", and the point at infinity Q' of that line l.
Let T be the intersection point t.P'Q', so that Q" is lying on P"T.
Then we find Q" as the intersection point of P"T and VQ'.

O16 Choose X" on c".
X' lies on VX", but also on P'Y', where Y" = P"X".s".
Since Y" lies on s", Y' is the point at infinity of VY".

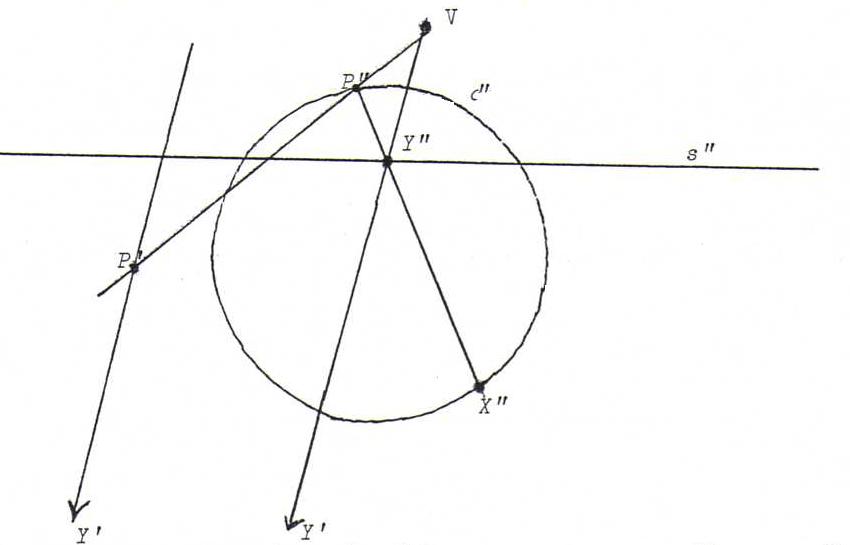
We have three cases: s" and c" have two, one or zero intersection points. Then c' becomes, respectively, a hyperbola, parabola or ellipse. We see this happen if we construct many pairs (X",X ' ), with X" on c".