CURSUS GRONDSLAGEN VAN DE MEETKUNDE

HOOFDSTUK ZES

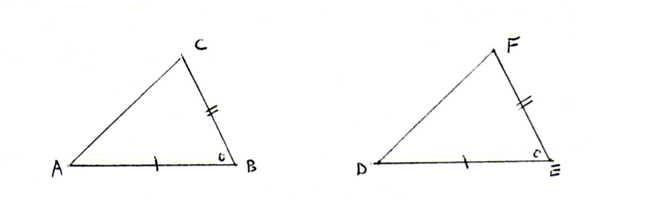
Definitie: we noemen de driehoeken ΔABC en ΔDEF 'congruent' (en noteren ΔABC ≅ ΔDEF) als [AB] ≅ [DE], [AC] ≅ [DF], [BC] ≅ [EF], ∠A ≅ ∠D, ∠B ≅ ∠E, ∠C ≅ ∠F.

Bij de opbouw van de meetkunde is het volgende axioma nodig:

ZHZ : ΔABC ≅ ΔDEF als [AB] ≅ [DE], ∠B ≅ ∠E, [BC] ≅ [EF].

Waarom is dit axioma onafhankelijk van de voorgaande axioma's?
Stel dat de lijnen ←AC→ en ←DF→ niet samenvallen. Verander de afstandsfunctie een klein beetje: maak op ←DF→ (en alleen op ←DF→) alle afstanden twee keer zo groot. Dan is nog steeds aan alle axioma's (oa ook het meetlat-axioma) voldaan, maar niet meer aan zhz (want niet meer [AC] ≅ [DF]).

Stelling 6.1 : als twee zijden congruent zijn, dan zijn de hoeken tegenover die zijden congruent.

Ofwel: gegeven ΔABC; als [AB] ≅ [AC], dan ∠B ≅ ∠C.

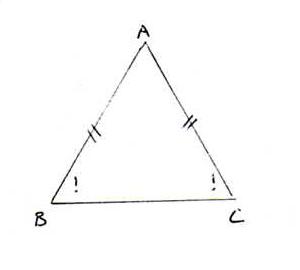
Bewijs: Omdat [BA] ≅ [CA], ∠A ≅ ∠A en [AC] ≅ [AB], is ΔBAC ≅ ΔCAB (zhz).
Dus ∠ABC ≅ ∠ACB.

Stelling 6.2 (hzh) : ΔABC ≅ ΔDEF als ∠A ≅ ∠D, [AB] ≅ [DE], ∠B ≅ ∠E.

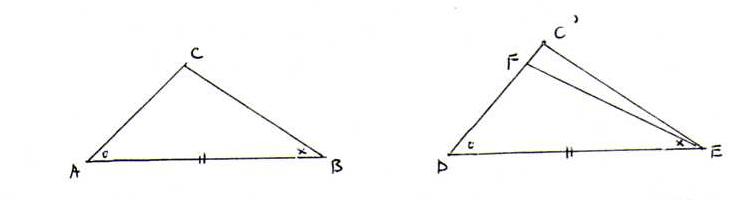
Bewijs: Kies op straal [DF→ een punt C' zo dat [AC] ≅ [DC'] (vgl stelling C2). Dan ΔABC ≅ ΔDEC' (zhz). Dus de stralen [EF→ en [EC'→ vallen samen (vgl de stelling in opgave 8.2). Dus F=C'(vgl stelling 2.1). Dus ΔABC ≅ ΔDEF.

Stelling 6.3 : als twee hoeken van een driehoek congruent zijn, dan zijn de zijden tegenover die hoeken congruent.

Bewijs: doe dit zelf mbv 6.2, analoog aan het bewijs van 6.1.

Stelling 6.4 (zzz) : ΔABC ≅ ΔDEF als [AB] ≅ [DE], [BC] ≅ [EF], [CA] ≅ [FD].

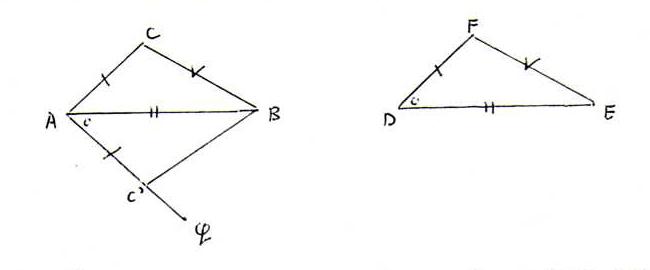
Bewijs: Laat [AQ→ de straal zijn, met Q aan de andere kant van lijn ←AB→ als C, zo dat ∠BAQ ≅ ∠EDF (vgl opgave 8.2). Laat C' op [AQ→ liggen zo dat [AC'] ≅ [DF].
Dan ΔEDF ≅ ΔBAC'(zhz). We moeten nog bewijzen ΔBAC' ≅ ΔBAC.

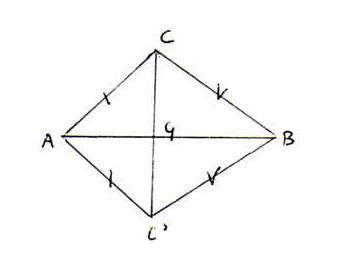
Welnu: Omdat C en C' aan verschillende kanten van lijn ←AB→ liggen, is er G op ←AB→ met C-G-C'.
Veronderstel nu A-G-B (andere gevallen gaan analoog, zie opgave 9).
∠ACG ≅ ∠AC'G en ∠BCG ≅ ∠BC'G (stelling 6.1). G ligt binnen ∠ACB en binnen ∠AC'B (ga na). Dus ∠ACB ≅ ∠AC'B (opgave 8.3).
Dus ΔACB ≅ ΔAC'B (zhz). Dus ΔBAC' ≅ ΔBAC.

OPGAVE 9: Bespreek de andere gevallen in het bewijs van stelling 6.4.

Als D binnen ∠BAC ligt en ∠BAD ≅ ∠CAD, dan heet de straal [AD→ een 'tweedeler' van ∠BAC.

Stelling 6.5 : iedere hoek heeft precies één tweedeler.

Bewijs:
Beschouw ∠BAC. Zonder verlies van algemeenheid mogen we aannemen [BA] ≅ [CA]. Laat D het middenpunt van [BC] zijn (vgl stelling C5), dus D ligt binnen ∠BAC.
Dan ΔABD ≅ ΔACD (zzz), dus ∠BAD ≅ ∠CAD. Dus [AD→ is een tweedeler van ∠BAC.

Anderzijds, stel dat [AE→ een tweedeler is van ∠BAC. Volgens stelling 4.7 (de kruisstelling) snijdt straal [AE→ segement [BC] in een punt D'.

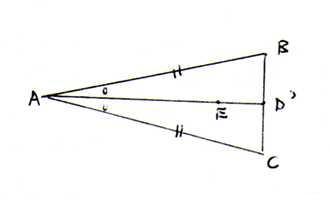
Dan ΔBAD' ≅ ΔCAD' (zhz). Dus [BD'] ≅ [CD']. Dus D' is middenpunt van [BC]. Volgens stelling C5 is D=D' en dus [AE→ = [AD→.

Stelling 6.6 : Gegeven een lijn l en een punt P niet op l. Dan is er een lijn door P die loodrecht staat op l.

Bewijs:
Neem A en C op l. Er is een punt Q aan de andere kant van l als P zo dat ∠PAC ≅ ∠QAC en [PA] ≅ [QA] (vgl opgave 8.2 en stelling C2).
Als P-A-Q dan vormen ∠PAC en ∠QAC een lineair paar en voldoet ←PQ→ (vgl de definities van 'loodrechte stand' en 'rechte hoek' in hoofdstuk 5).

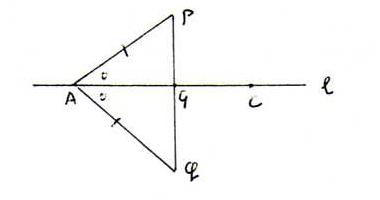
In het andere geval: laat G het punt op l zijn met P-G-Q. Dan G≠A en ΔPAG ≅ ΔQAG (zhz). Dus ∠AGP ≅ ∠AGQ. Omdat deze twee hoeken ook een lineair paar vormen, zijn ze beide recht.

We kunnen mbv axioma M2 ook eenvoudig bewijzen dat door een punt P op een lijn l een lijn gaat die loodrecht staat op l. Maar we willen dat we dit axioma later kunnen laten vallen.