CURSUS GRONDSLAGEN VAN DE MEETKUNDE

HOOFDSTUK VEERTIEN

We kijken vandaag naar eenvoudige stellingen van de hyperbolische meetkunde.
We maken daarbij onderscheid tussen enerzijds stellingen die alleen in het model van Poincaré gelden, en anderzijds stellingen die uit de axioma's van de absolute meetkunde en het axioma van de hyperbolische meetkunde worden afgeleid en dus in alle modellen van de hyperbolische meetkunde geldig zijn.

Stelling 14.1 : In de hyperbolische meetkunde is de hoeksom van de hoeken in een driehoek altijd kleiner dan twee rechte hoeken.

Bewijsschets: Er is een driehoek Δ ABC waarvan de som der hoeken kleiner is dan twee rechte hoeken, dus met positief hoekdefect (zie stelling 9.11 en stelling 10.3).

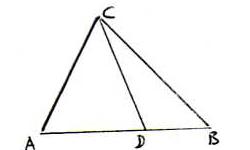
Deze kunnen we onderverdelen in twee driehoeken ΔADC en ΔBDC met A-D-B; omdat hoekdefect additief en niet-naegatief is (zie hoofdstuk 11 en stelling 9.11), heeft minstens één van deze twee driehoeken positief hoekdefect. Zo voortgaande vindt men driehoeken met willekeurig kleine zijden en positief hoekdefect. Stel nu dat ΔPQR een willekeurige driehoek is. Dan kan men binnen ΔABC een 'deeldriehoek' vinden met positief hoekdefect d en zo dat er binnen ΔPQR een congruente deeldriehoek bestaat. Deze heeft hoekdefect d, en dus heeft ΔPQR hoekdefect minstens d.

Hieronder een schets van een 'grensdriehoek' in het model van Poincaré waarvan de hoeksom 0 is. Omdat de 'hoekpunten' op {y=0} liggen, zijn het geen echte h-punten.

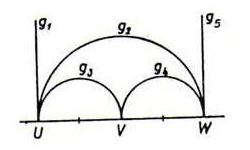
Maar als men ze iets verschuift, vindt men een 'echte' driehoek waarvan de hoeksom maar weinig groter dan 0 is.

Bij de volgende stelling bestaat wel een soortgelijke stelling voor de hyperbolische meetkunde in het algemeen, maar we formuleren en bewijzen haar alleen voor het model van Poincaré.

Stelling 14.2 : In het model van Poincaré bestaat bij twee hyperparallellen altijd precies één lijn die beide parallellen loodrecht snijdt.

Bewijsschets: Zie schets hieronder; j is de machtlijn van g₁ en g₂.

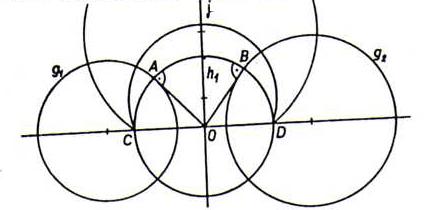
De e-cirkels loodrecht op g₁ en g₂ vormen de elliptische bundel door C en D.
Van deze is alleen h (met e-middelpunt O op y=0) een h-lijn.
Deze h is ook de enige h-lijn loodrecht op g₁ en j.

OPGAVE 25: Bewijs dat in de hyperbolische meetkunde bij twee parallelle lijnen hoogstens één lijn bestaat die beide parallellen loodrecht snijdt.

Merk op dat in de euclidische meetkunde bij twee parallelle lijnen altijd oneindig veel lijnen bestaan die beide loodrecht snijden. Ook de volgende stelling staat in contrast met de euclidische meetkunde.

Stelling 14.3 : Zij g een h-lijn met grenspunten U en V in het model van Poincaré. dan vormen de punten aan één kant van g op een bepaalde vaste afstand van g een e-cirkelboog g^* door U en V. Deze punten liggen dus niet op een h-lijn.

Bewijsschets: Zij g^* een willekeurige e-cirkelboog door U en V. Zie de schets hieronder.

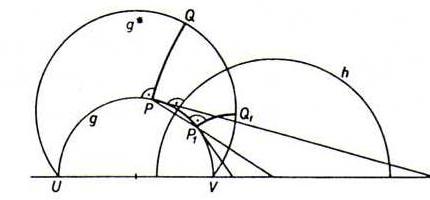
Stel dat de h-loodlijnen op g uit P en P₁ g^* snijden in Q en Q₁.
Zij h de middelloodlijn van [PP₁]. Deze staat ook loodrecht op g^*, dus onder spiegeling in h gaat segment [PQ] over in segment [P₁Q₁]. Dus L(P,Q) = L(P₁,Q₁).

Uit stelling 14.3 volgt ook dat met de axioma's van de absolute meetkunde alleen, dus zonder het parallellenaxioma, niet bewezen kan worden dat de punten die op een bepaalde vaste afstand van een lijn l liggen twee lijnen parallel met l vormen, en dus ook niet dat parallelle lijnen equidistant zijn.

OPGAVE 26: Waar liggen de punten die een vaste afstand hebben tot een h-lijn op een e-straal? Bewijs.

Stelling 14.4 : In het Poincarémodel vormen de punten op een bepaalde vaste afstand van een gegeven h-punt een e-cirkel. Maar het hyperbolische middelpunt is verschillend van het euclidische middelpunt.

Bewijsschets: Bekijk de volgende figuur die alles vertelt.

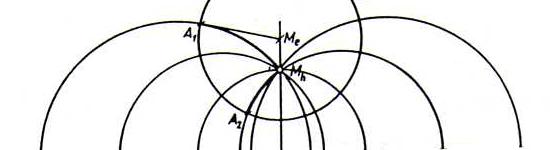
De h-lijnen door M_h snijden K loodrecht. Dat L(M_h,A₁) = L(M_h,A₂) volgt door spiegelen in de tweedeler van ∠A₁M_hA₂.

Stelling 14.5 : (congruentiestelling hhh)
In de hyperbolische meetkunde zijn twee driehoeken met paarsgewijs congruente hoeken altijd congruent.

Bewijs: Stel dat ΔABC en ΔA'B'C' zulke driehoeken zijn.
Als [AC] niet congruent is met [A'C'], kunnen we een punt A₁ ≠ A op ←AC→ vinden zo dat [A₁C] ≅ [A'C']. Neem aan dat A₁C kleiner is dan AC, of anders kunnen de rollen der twee driehoeken verwisseld worden.

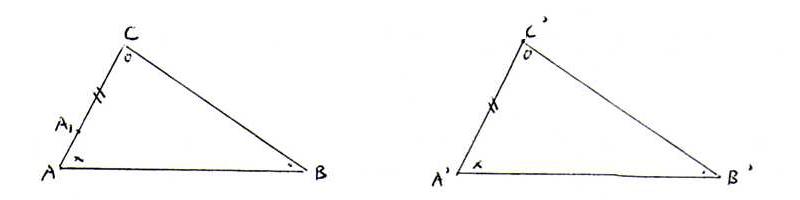
Evenzo is er een punt B₁ op ←BC→ zo dat [B₁C] ≅ [B'C'].
Als B₁=B dan ΔA₁CB ≅ ΔA'B'C' (zhz), dus ∠A₁BC ≅ ∠A'B'C' ≅ ∠ABC. Dat is strijdig met axioma M2 (opgave 8.2). Dus B₁ ≠ B.
Stel nu dat CB₁ groter is dan CB, als in de volgende schets.

Dan snijdt segment [A₁B₁] segment [AB] in een inwendig punt D (zie opgave 7).
Dan ΔA₁CB₁ ≅ ΔA'C'B' (zhz), dus ∠CA₁B₁ ≅ ∠C'A'B' ≅ ∠CAB. Dit is strijdig met stelling 7.1.
Dus is CB₁ kleiner dan CB, als in de volgende schets.

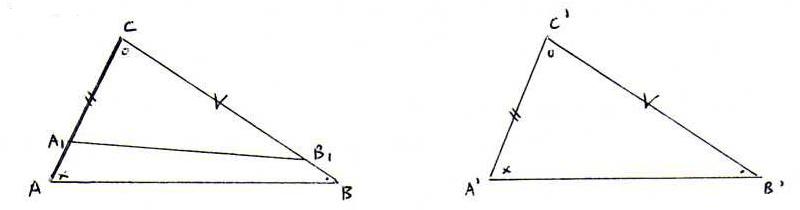
Nu is het hoekdefect in ΔABC gelijk aan de som van de hoekdefecten in ΔA₁CB₁, ΔA₁BB₁ en ΔAA₁B. Omdat die hoekdefecten positief zijn, is het hoekdefect van ΔA₁B₁C kleiner dan dat van ΔABC, dus ook kleiner dan dat van ΔA'B'C' (omdat ΔABC en ΔA'B'C' congruente hoeken hebben).
Maar ΔA₁B₁C ≅ ΔA'B'C' (zhz). Tegenspraak.
Dus [AC] ≅ [A'C']. Dus ΔABC ≅ΔA'B'C'(zhh).