CURSUS GRONDSLAGEN VAN DE MEETKUNDE

HOOFDSTUK DERTIEN

We bekijken het model van Poincaré (1854-1912) voor hyperbolische meetkunde.

Het 'hyperbolische vlak' is het vlakdeel boven de x-as in het x,y-vlak.
De punten van dat vlakdeel zijn 'hyperbolische punten'. De punten op de x-as doen niet mee, maar heten 'grenspunten'.
De 'hyperbolische lijnen' zijn: de halve cirkels met middelpunt op de x-as en de halfrechten parallel aan de y-as.
Om hyperbolische punten en lijnen te onderscheiden van euclidische spreken we van h-punten en h-lijnen, e-punten en e-lijnen en e-cirkels.

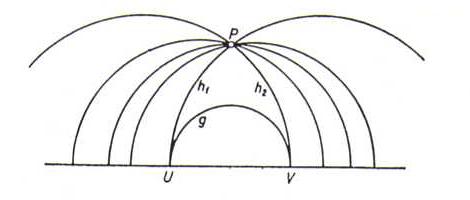
Er is niet voldaan aan het parallellenaxioma:

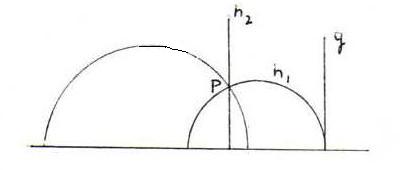
In elk van beide plaatjes hierboven en hieronder zijn alle geschetste h-lijnen door P parallel aan g. (De h-lijnen h₁ en h₂ heten 'grensparallel', de andere h-lijnen 'hyperparallel'.)

Zij [AB] een h-segment op een e-cirkel. Beschouw het volgende plaatje:

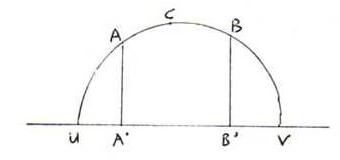
De 'dubbelverhouding' A'B'UV is (A'U/A'V):(B'U/B'V).
De 'hyperbolische afstand' tussen A en B is L(A,B) := | (1/2) log (A'B'UV) | = (1/2) log (A'B'VU).
Merk op dat voor C tussen A en B geldt L(A,B) = L(A,C) + L(C, B); werk dit uit.

Zij [AB] een h-segment op een e-lijn. Zie plaatje hieronder:

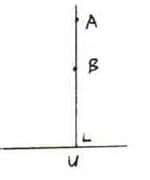
De 'hyperbolische afstand' tussen A en B is | log (AU/BU) | .

Hoeken worden op de euclidische manier gemeten. (Zie plaatje hieronder.) We hebben in hoofdstuk twaalf al gezien dat hoekmaat invariant is onder spiegeling in een e-cirkel.

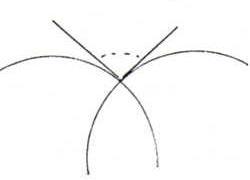
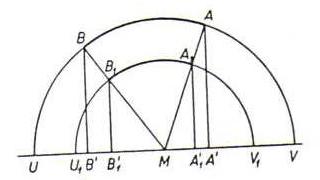
De hyperbolische afstand tussen twee punten is invariant onder translatie parallel aan de x-as.

Als de h-lijn door twee punten een halve e-cirkel is, is de afstand ook invariant onder euclidische puntvermenigvuldiging vanuit het middelpunt van deze e-cirkel. Ga dit na mbv de volgende schets:

De hyperbolische afstand is ook invariant onder spiegeling in een h-lijn. Zie hiervoor de volgende plaatjes:

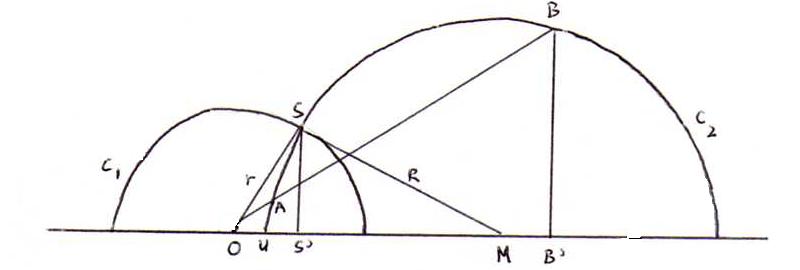
Om na te gaan dat L(S,A) = L(S,B), dus dat C₁ 'middelloodlijn' van het h-segment AB is, kan men als volgt te werk gaan:

C₁: x² + y² = r² ; C₂: (x-m)² + y² = R² (met m² = r² + R²).
Men kan analytisch controleren dat S'A'UV = S'B'UV.

Ook in de volgende gevallen blijft de afstand bewaard onder spiegeling in C₁ (dit kan men bewijzen mbv analytische meetkunde):

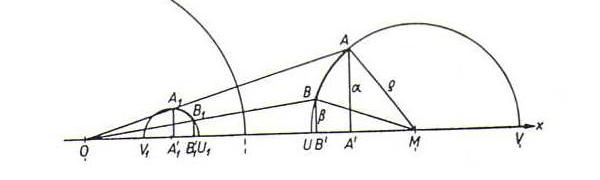
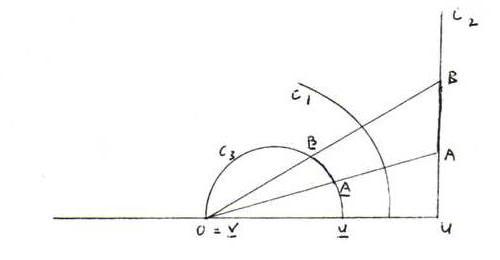
In het plaatje hieronder ziet u hoe men bij een gegeven h-segment [AB] en een gegeven h-lijn g en een gegeven punt C op g een segment {CD] op g kan 'construeren'dat congruent is met [AB]:

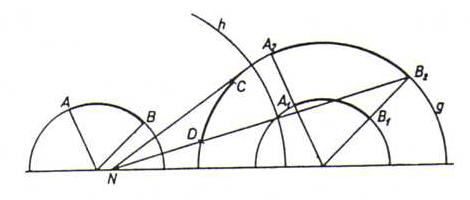
[AB] → (translatie) → [A₁B₁] → (puntvermenigvuldiging) → [A₂B₂] → (spiegeling in middelloodlijn van [CA₂]) → [CD].

(Als g een e-straal is, kan men [AB] eerst 'overbrengen' naar een h-segment op een e-cirkel:)

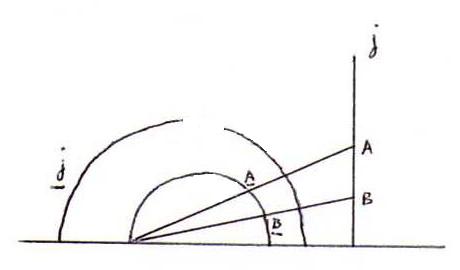
OPGAVE 24: Laat zien dat het model van Poincaré voldoet aan ale axioma's van de absolute meetkunde.