2. BOOGLENGTE

Definitie 10: Een kromme is het bereik van een afbeelding I→ℜ³, waarbij I een interval is op de reële as. We veronderstellen steeds stilzwijgend dat de afbeelding zo vaak continudifferentieerbaar is als nodig is voor de geldigheid van onze bewereingen.
We schrijven het beeld van t als x(t) = (x₁(t),x₂(t),x₃(t)).
Merk op dat verschillende afbeeldingen (verschillende parametriseringen) dezelfde kromme kunnen definiëren. Zo wordt de cirkel door (cos(t),sin(t),0) en door (sin(2t),cos(2t),0) gegeven.

Voorbeeld 11:
1) rechte: x(t) = s + t v;
2) cirkelschroeflijn: x(t) = (a.cos(t),a.sin(t),bt), doorsnede van rechte cirkelcilinder x₁²+x₂²=a² en golfplaatcilinder x₂=a.sin(x₃/b);
3) kubische parabool: x(t) = (t, t², t³), doorsnede van de parabolische cilinder x₂=x₁² en de kubische cilinder x₃=x₁³.

Definitie 12: een singulier punt van een kromme met parametrisering x(t) is een punt x(t₀) waar x'(t₀)=0. Een punt dat niet singulier is heet regulier. Zie ook opgave 13.
Stel dat x(t₁) een regulier punt is. Dan geldt x(t) = x(t₁) + (t-t₁)x'(t₁) + O((t-t₁)²). De lijn met parametervoorstelling x(t₁) + λx'(t₁) heet raaklijn in x(t₁) aan de kromme x(t), en de richtingsvector x'(t₁) heet raakvector.
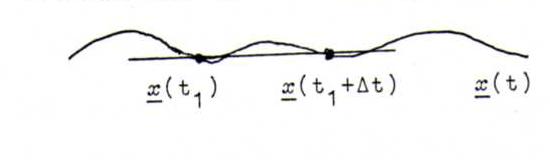
Dit kan men ook meetkundig verklaren:

De verbindingslijn heeft richtingsvector (x(t₁+Δt)-x(t₁))/Δt.
Als Δt→0 gaat de verbindingslijn over in de raaklijn en de richtingsvector in x'(t₁).

Opgave 13: Substitueer t=u³ in voorbeeld 11 3). Laat zien dat men dan dezelfde kromme krijgt, die bij deze parametrisering echter een singulier punt heeft.

Opgave 14: Bepaal in de voorbeelden 11 2) en 11 3) het snijpunt van de raaklijn in x(t₁) met het vlak x₁=0. Voor welke t₁ is dat snijpunt oneigenlijk?

Definitie 15: De lengte over de kromme x(t) tussen t₀ en t wordt benaderd door tussen t₀ en t een stel punten t_k te nemen en te kijken naar Σ ||x(t_k+1)-x(t_k)||.

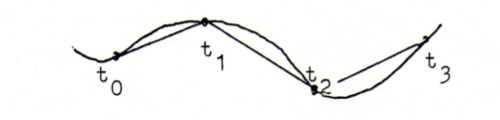
Deze uitdrukking is gelijk aan Σ ||x'(τ_k)(t_k+1-t_k)||, waarbij τ_k tussen t_k en t_k+1.
Limiet nemen rechtvaardigt dan de volgende definitie van de booglengte van x(t₀) tot x(t):
s(t) = _t0∫^t ||x'(τ)|| dτ = _t0∫^t √(x₁'(τ)²+x₂'(τ)²+x₃'(τ)²) dτ.

Volgens de hoofdstelling van de integraalrekening is dan ds/dt = ||x'(τ)||, en hieruit volgt ||d/ds x(s)|| = ||x'(t)|| dt/ds = 1.

We zullen voortaan noteren x ^.(s) in plaats van d/ds x(s), zodat men aan het puntje kan zien dat de afgeleide naar de booglengte wordt bedoeld.

Volgens definitie 12 is de raaklijn in x(s₁) dan x(s₁)+λx ^.(s₁), waarbij de raakvector x ^.(s₁) lengte 1 heeft.

Opgave 16: Geef een parametervoorstelling van de cirkelschroeflijn met de booglengte als parameter. Geef ook de raakvector.

Opgave 17: Geef een parametervoorstelling van de vlakke kromme y=x^3/2, met de booglengte als parameter.

Opgave 18: Bereken de booglengte van de cycloïde a(t-sin(t),1-cos(t)), en teken deze kromme.
Deze beschrijft de baan van een punt P op een cirkel die over een rechte lijn rolt. Laat dat zien.

Opgave 19: Bepaal f(t) zó dat de kromme x(t) = f(t)(cos(t),sin(t),1) op de kegel x₁²+x₂²=x₃² de beschrijvenden van deze kegel snijdt onder een constante hoek.

Opgave 20: Laat een kromme gegeven zijn met twee parametrizeringen met parameters t en s respectievelijk, zodat x(s) = x(t(s)) en x(t) = x(s(t)).
Laat x'' de tweede afgeleide zijn naar t, en x ^.. de tweede afgeleide naar s.
Druk ||x ^..|| uit in x' en x''.

(Uitkomst ||x ^..|| = ||x'⊗x''||/||x'||³. Deze uitkomst is van belang voor de berekening van de kromming, zoals in de volgende paragraaf beschreven.)

uitwerkingen