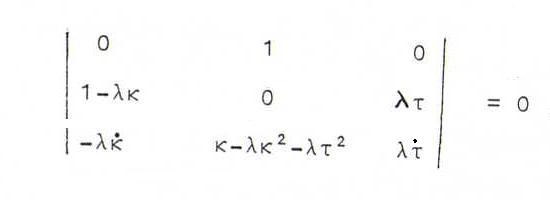
, so τ . (1-λκ) = -λκ . τ.
So τ=0 or κ is constant (and τ is constant or λ = 1/κ) or τ . /τ = (λκ . )/(λκ-1) (then τ = d(λκ-1) with d≠0).
DIFFERENTIAL GEOMETRY COURSE
7. CURVES OF BERTRAND
Definition 67: If a curve x(t) has the property that its principal normals are also principal normals of an other curve y(t), we call it a curve of Bertrand.
Then both curves together form a pair of Bertrand curves.
Proposition 68: The curve x(t) is a curve of Bertrand if and only if it satisfies a natural equation of the form aτ+bκ=c (a,b,c≠0) or τ=0
(planar curve with an infinite number of partners) or κ=c (then there is an infinite number of partners if τ is also constant; in the other case, y(t) exists of the curvature
centers of x(t)).
Proff: We must have y(s)=x(s)+λ(s)n(s) (s is arc length of x(s), but in general not arc length of y(s)).
Now y '(s) must be perpendicular to n(s), and the three vectors y '(s),y''(s) and n(s) must lie in one plane.
Now y ' = x . + λ . n + λ(-κt+τb). If y ' is perpendicular
to n, we find λ . =0, so λ is constant.
Then y'' = (-λκ .)t + (κ-λκ2-λτ2)n +
(λτ .)b. We have
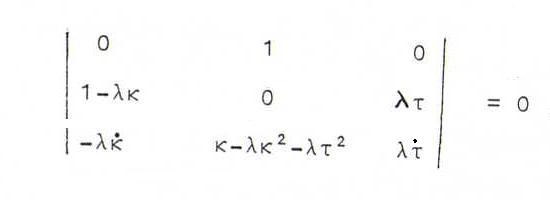
, so τ . (1-λκ) = -λκ . τ.
So τ=0 or κ is constant (and τ is constant or λ = 1/κ) or τ . /τ = (λκ . )/(λκ-1) (then τ =
d(λκ-1) with d≠0).
Example 69: The circular helix (see 16 and 46) has partners y(t) = ((a-λ)cos(t), (a-λ)sin(t), bt).
Problem 70 : Prove that if x(t) and y(t) are corresponding curves of Bertrand, then the angle between corresponding tangents is constant. For which curves is
this constant angle 90 degrees?
Problem 71 : Prove that, if a curve x(s) has constant curvature κ(s), then the curve y(s) of the curvature centers of x(s) has a constant curvature, too. In this case, x(s) is the curve existing of the curvature centers of y(s). Also provre that the product of the torsions in corresponding points is constant.
Problem 72 : In each point P of a curve K we choose on the principal normal a point Q. If P runs through the curve K, then Q describes the curve C. In each point Q, the osculating plane of C coincides with the normal plane of K in P. Prove that K has constant curvature.
Problem 73 : A necessary and sufficient condition that the binormals of a curve be principal normals of another curve, is that there exists a constant λ≠0 such that λ2κτ2 = -κ + λτ .. Prove this.
Opgave 74 : Suppose we have a curve whose binormals are also binormals of a second curve. Prove the curve is planar and both curves are congruent.
Opgave 75 : The rectifying planes of a curve k are parallel to a fixed straight line l. Give an example of such a curve.
Prove that for all n in No we have τ(n)κ(n+1)=κ(n)τ(n+1). Here f(m) denotes the m-th derivative of f as a function of s.