DIFFERENTIAL GEOMETRY COURSE
4. SERRET AND FRENET
Definition 30: The osculating plane (kissing plane) in a point x(t0) of the curve x(t) is the limit of the position of the plane through the tangent in
x(t0) and a neighbour point x(t0+Δt) on the curve, when Δt→0.
Proposition 31: The osculating plane in x(t0) is the plane with parameter representation
x(t0)+λx'(t0)+μx''(t0) and equation
det(x-x(t0),x'(t0),x''(t0)=0.
Prove: Since x(t0+Δt)-x(t0)=x'(t0)+(1/2)x''(t0)Δt2
(+ terms of higher degree), the equation det(x-x(t0),x'(t0),x(t0+Δt)-x(t0))
= 0 becomes, when Δt→0, the equation det(x-x(t0),x'(t0),x''(t0)=0.
Definition 32: We call a point x(s0) on a curve x(s) whose parameter s is arc length, an inflection point of the curve if κ(s) changes sign in
s0 (then the local curvature vector is 0).
Proposition 33: In the inflection points of the curve x(t), the vectors x' and x'' have either the same direction or opposite directions.
Prove: According to problem 20 we find : x .. = 0 ↔ x'⊗x'' = 0.
Problem 34: Determine the equation of the osculatiom plane in an inflection point.
Problem 35: Give the equation of the osculating plane in a point x(t) of the cubic parabola from example 11 iii).
Definition 36: (Serret-Frenet frame)
Let x(s) be a curve whose parameter s is arc length.
Let t(s) := x .(s) be the tangent of length 1. Choose the principal normal vector n(s) with length 1,
having the same or opposite direction as the curvature vector x ..(s), as we discussed in the previous section.
So the osculating plane is x(s)+λt(s)+μn(s).
Start with t(s),n(s) and complete the frame with the so-called binormal
vector b(s) so as to get a right orthonormal frame (that is to say: b := t⊗n).
Then we call t,n,b The Serret-Frenet frame.
We call the plane x(s)+λn(s)+μb(s) the normal plane, and the plane x(s)+λt(s)+μb(s) the rectifying
plane.
Problem 37: Determine the equations of these three planes in an arbitrary point of the cubic parabola.
Proposition 38 (Theorem of Serret and Frenet):
There exist functions κ(s) and τ(s) with
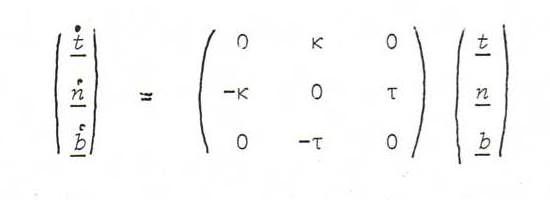
Prove: The function κ is the curvature function, and we discussed the formula t . = κn in the previous section.
According to problem 9b), n is perpendicular to n ., so according to problem 8 there exist ρ and τ such that n . =
ρt+τb. Again according to problem 8, we have ρ=n ..t.
Using n.t=0 we see by differentiation n ..t+n.t . = 0, so
ρ = n ..t = -n.t . = -κ.
Likewise: since b is perpendicular to b ., we have b . = αt+βb.
Then α = b ..t = -b.t . = 0, and β = b ..t =
-b.n . = -τ.
Definition 39: The function τ from the theorem of Serret and Frenet is called the torsion of the curve.
Proposition 40: κ2τ = det(x .,x ..,x ...).
Prove: Using x .. = κn we find x ... = κ .n +
κn . = κ .n + κ(-κt+τb), so
det(x .,x ..,x ...) =
det((1,0,0),(0,κ,0),(-κ2,κ .,κτ)) = κ2τ.
Problem 41: Prove that det(x',x'',x''') = ||x'||6det(x .,x ..,x ...),
and deduce:
τ = det(x',x'',x''')/(x'⊗x'')2
answers
HOME