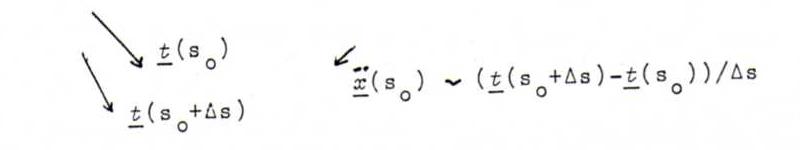
CURSUS DIFFERENTIAALMEETKUNDE
3. CURVATURE
Definition 21: Given a curve with arc length as parameter: x(s). Let t(s) be the tangent vector, so t(s) = x .(s).
We define the curvature vector to be the derivative of the tangent vector, that is x ..(s). This curvature vector is for every s perpendicular to the tangent vector
(see problem 9).
We can see by the changing tangent vector in which direction the curvature vector is pointing:
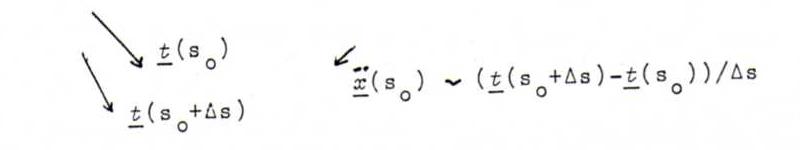
Now we choose for every s a vector n(s) (called principal normal vector) with length 1 which has the same direction or the opposite direction as x ..(s),
in such a way that n(s) becomes a continuous vector field.
Note that this can be done in two ways. For planar curves we see:
The curvature vector becomes 0 and changes its direction in an inflection point,

The principal normal vector keeps its length 1 and stays at one side of the curve.

So for each s there is a number κ(s) so that x ..(s) = κ(s)n(s).
We call κ(s) the curvature function of the given curve. The curvature changes its sign in an inflection point, and its absolute value is the length of the curvature vector.
We define the curvature radius R(s) to be 1/κ(s) (∞ in an inflection point), and the curvature center to be x(s)+R(s)n(s). These are the center and the radius
of the so-called curvature circle, about which we are going to speak later on. The curvature vector x ..(s) is always pointing from the point x(s)
to the curvature center.
Explanation 22: The curvature is a measure for the change of the direction of the tangent vector:
Let Δφ be the angle between t(s) and t(s+Δs). Then
||t(s+Δs)-t(s)|| = √((t(s+Δs)-t(s)).(t(s+Δs)-t(s))) = √(2-2t(s+Δs).t(s))
= √(2-2cos(Δφ)) = 2|sin(Δφ/2)|.
So |κ(s)| = ||x ..(s)|| = lim (Δs→0) 2|sin(Δφ/2)|/Δs = lim (Δs→0) Δφ/Δs.
Explanation 23: About the curvature circle.
The circle r(cos(t),sin(t)) becomes with arc length as parameter: (cos(s/r),sin(s/r)). Hence it follows that the curvature satisfies κ(s) = ||x ..(s)|| = 1/r.
Now let x(s0) be a point of the curve x(s). Its curvature center is m(s0) =
x(s0)+R(s0)n(s0).
The curvature circle has parametrisation
m(s0)+R(s0)(sin((s-s0)/R(s0))t(s0)-cos((s-s0)/R(s0))n(s0))
(= c(s)).
So this circle lies in the plane x(s0)+λt(s0)+μn(s0) (called osculation plane or kissing plane,
about which we are going to speak later on). It is passing through
x(s0) and there it is tangent to x(s), and it has in s0 the same curvature as the curve x(s): see the following problem.
Problem 24: Prove that s is also arc length of the circle c(s), and that c(s0)=x(s0), c .(s0)=x .(s0), c ..(s0)=x ..(s0)
Here are two theorems about the curvature function that we don't prove. We can prove the second one by generalizing example 27 which comes immediately after it.
Proposition 25: κ(s) is invariant under motion (that is to say: invariant when the curve is stiffly moved through space).
Proposition 26: With any given curvature function there is a planar curve having this curvature. This curve is unique up to rotations and translations.
Example 27: (as an illustration of proposition 26).
Let κ(s)=s, and x(s) a planar curve with this curvature. (We are going to determine this curve.)
Because ||x .(s)||=1, we have x .(s)=(cos(α(s),sin(α(s)), so κ(s)=α .(s).
Hence α(s)=(1/2)s2+c and x(s)=(d∫s cos((1/2)σ2+c) dσ,
d'∫s sin((1/2)σ2+c) dσ).
When we choose an other c this means we rotate the curve, when we choose an other d and d' we translate the curve.
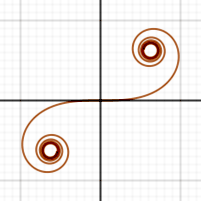
This curve is called clotoid (spiral of Cormi). Since 0∫∞ cos((1/2)σ2) dσ = 0∫∞ sin((1/2)σ2)
dσ = (1/2)√π, it looks like this:
For planar curves in the x,y-plane we always have: κ(s) is the derivative with respect to arc length s of the angle between the tangent vector of length 1 and the x-axis.
Problem 28: Determine the curvature of the cycloid (see problems 18 and 20) as a function of s.
Problem 29: Prove that the straight lines are the curves with curvature function κ(s)=0.
Thereafter, prove that, whenever the tangents of a curve go through a fixed point, or are all
parallel, this curve must be a straight line.