COURSE OF DIFFERENTIAL GEOMETRY
22. CONCLUSION
The following last proposition is a simplified version of the wellknown Gausz-Bonnet theorem.
This theorem is related to the theorems of Gausz, Stokes and Green in Analysis.
The content of the Gausz-Bonnet theorem was already known to Carl Friedrich Gausz (1777-1855), but unproven until O.Bonnet (1819-1892) proved it.
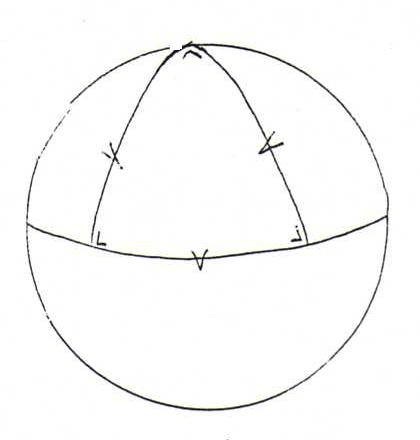
Proposition 193: Given three points on a surface. Let G be the geodetic triangle confined by the shortest-way-geodesics between these three points. Then the surface integral of total
curvature over G is equal to the angle excess α + β + γ - π (α, β, γ are the angles between the tangents to the geodetic sides of this triangle in the vertices).
Example 194: On a sphere with radius R, total curvature is in each point 1/R2. The area of a geodetic triangle with three right angles, one vertex on the north pole and two on the
equator, is 4πR2/8, whilst the angle excess is equal to 3π/2-π. So the Gausz-Bonnet theorem holds in this case.

See here a more general discussion of angle excess on a sphere.
Remark 195: The surface of revolution of the tractrix has a constant negative curvature, and is therefore called 'pseudo-sphere'.
So a geodetic triangle on this pseudo-sphere always has a negative angle excess.
See here a popular discussion of the role of sphere and pseudo-sphere in non-euclidean geometry.
Remark 196: We already met the tractrix (drag curve) in 153.
The parametrisation is (u,0,f(u)) with f(u) = + ∫cu √(c2-y2)/y dy.
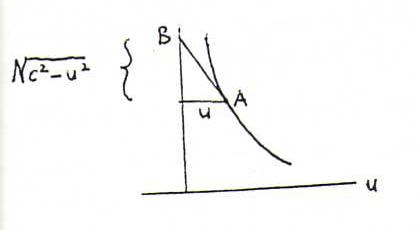
(Here d(A,B)=c; check that the graph of f is the traject of a dog that keeps running after a hare at a constant distance c, whilst the hare is fleeing along the y-axis.)
Problem 197: Check by calculation that the total curvature of the pseudo-sphere is constant and equal to -1/c2.