DIFFERENTIAL GEOMETRY COURSE
15. THE SECOND FUNDAMENTAL FORM
Definition 132 : Let x(u,v) be a surface, and N(u,v) the normal with length 1 (in the direction of xu⊗xv).
Let hi j = xuiuj . N (with u1 = u, u2 = v).
Then we call h1 1 (du)2 + 2 h1 2 du dv + h2 2 (dv)2 the second fundamental form.
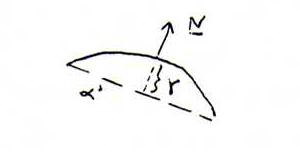
Explanation 133 : Let α be the tangent plane in the point xo with parameter values uo and vo, and α ' the plane parallel to
α at a (little) distance γ from α, and let k be the intersection curve of α ' and the surface.

For the points on k we have x = x(u,v) and (x - xo + γN) . N = 0.
Using Taylor we find x - xo = xu du + xv dv + (1/2) xu u (du)2 +
xu v du dv + (1/2) xu v (dv)2.
Since xu and xv are perpendicular to N, the equation becomes in second order approximation:
((1/2) xu u (du)2 + xu v du dv + (1/2) xu v (dv)2) . N = - γ, so
h1 1 (du)2 + 2 h1 2 du dv + h2 2 (dv)2 = -2γ.
This is (in coordinates with respect to a not necessarily orthonormal base xu , xv) the equation of a conic, in which the right hand side
is the second fundamental form.
Definition 134 : We call the conic h1 1 (du)2 + 2 h1 2 du dv + h2 2 (dv)2 = 1 indicatrix of Dupin.
After the kind of the indicatrix we distinguish:
1. hyperbolic points: det(hi j) negative. (Then we can resolve the form in linear factors, and Σ hi j du dv = 0 gives the asymptotic directions, see our course of projective geometry).
2. parabolic points: det(hi j) = 0. (Indicatrix exists of two parallel lines; for example (2du + 3dv)2 = 1 gives du = +(1/2) - (3/2)dv, so indicatrix xu (+(1/2) - (3/2)t) + xv t.
3. elliptic points: det(hi j) positive. (Then we can't resolve the form and there are no asymptotes).
Problem 135 : Do you know a surface on which each point is navel point (umbilical point), that is: the indicatrix is in each point a circle?
Check this by calculation.
Do you know a surface on which each point is planar, that is: the second fundamental form is everywhere the 0-form? Check this by calculation.
Problem 136 : Determine the second fundamental form of the torus and check that det(hi j) = R cos(φ) (r + R cos(φ)).
Deduce that the points at the inner side of this inner tube of a bicycle are hyperbolic, and the points at the outer side elliptic. The points on the circles φ = +π/2 are parabolic.
Problem 137 : Consider the right helicoid surface ((a+u)cos(v), (a+u)sin(v), bv), see 128.
Show that the parameter lines are asymptotice lines (that is: they have in each point an asymptotic direction), and form an orthogonal net, so each point is hyperbolic with an orthogonal hyperbola as
its indicatrix.
Problem 138 : Prove that a1 1h2 2 - 2 a1 2h1 2 + a2 2h1 1 = 0 is the necessary and sufficient condition so that in each hyperbolic point the indicatrix is an orthogonal hyperbola. (See proposition 120.)