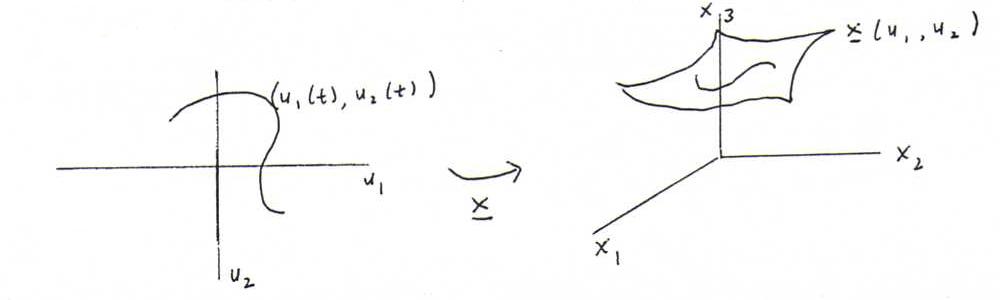
The image curve has parametrisation x(u1(t),u2(t)), short x(t).
The arc length s of x(t) satisfies ds/dt = ||x '(t)|| = ||xu1 du1/dt + xu2 du2/dt|| ; hence it follows that (ds)2 = xu1 du1 . xu1 du1 + 2 xu1 du1 . xu2 du2 + xu2 du2 . xu2 du2.
DIFFERENTIAL GEOMETRY COURSE
12. THE FIRST FUNDAMENTAL FORM
Explanation 103 : We have to consider differentials first.
If f = f(x) then df = f '(x) dx ; for example, if f = cos(x) then df = -sin(x) dx ; df is the first order approximation of Δf := f(x+dx) - f(x) (calculate df and Δf in the example, with
x = π/2, dx = 0.001).
If f = f(x,y) then df = fxdx + fydy ('total differential') ; for example, if f = x/y then df = (1/y)dx -(x/y2)dy ;
df is the first order approximation of Δf := f(x+dx,y+dy) - f(x,y).
Explanation 104 : Now we have to consider curves on the surface.

The image curve has parametrisation x(u1(t),u2(t)), short x(t).
The arc length s of x(t) satisfies ds/dt = ||x '(t)|| = ||xu1 du1/dt + xu2 du2/dt||
; hence it follows that (ds)2 = xu1 du1 . xu1 du1 +
2 xu1 du1 . xu2 du2 +
xu2 du2 . xu2 du2.
Definition 105 : We define the first fundamental form of the surface by (ds)2 = a1 1 (du1)2 + 2 a1 2 du1 du2 + a2 2 (du2)2, where ai j = xui . xuj.
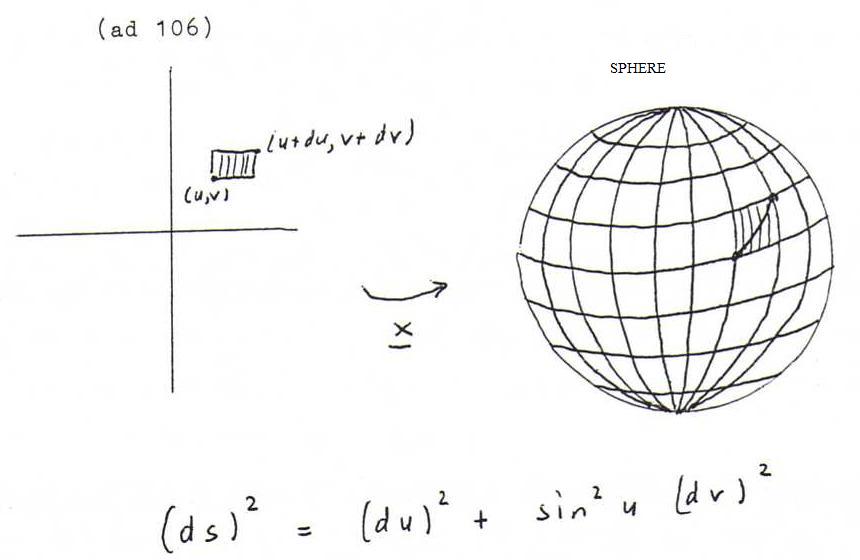
Examples 106 :
Plane: x(u,v) = (u,v,0). Then (ds)2 = (du)2 + (dv)2 ; this corresponds to the theorem of Pythagoras.
Sphere: x(u,v) = (sin u cos v, sin u sin v, cos u) ; here (ds)2 = (du)2 + sin2u (dv)2 ; see the picture at the end of this section 12.
Graph of a function: x(u,v) = (u,v,f(u,v); then
(ds)2 = (1+fu2) (du)2 + 2 fufv du dv + (1+fv2) (dv)2.
For each surface we have: a1 2 = 0 in the points where the parameter lines are perpendicular to each other.
Explanation 107 : We will now see that the first fundamental form determines the metrics of the surface:
i) The arc length of a curve on the surface, say x(u1(t),u2(t)), t ∈ (t0,t1), is
s(t0)∫s(t1) ds = t0∫t1 ds/dt dt =
t0∫t1 √(Σ ai j dui/dt duj/dt) dt.
ii) The angle between two curves on the surface, say x(a1(t),a2(t)) and x(b1(t'),b2(t')), is φ with
cos(φ) = (xu1 da1/dt + xu2 da2/dt) .
(xu1 db1/dt' + xu2 db2/dt' ) /
( || xu1 da1/dt + xu2 da2/dt ||
|| xu1 db1/dt' + xu2 db2/dt' || ) =
= ( a1 1 + a1 2 db2/db1 + a2 1 da2/da1 + a2 2 da2/da1 db2/db1 ) /
( √(a1 1 + 2 a1 2 da2/da1 + a2 2 (da2/da1)2)
√(a1 1 + 2 a1 2 db2/db1 + a2 2 (db2/db1)2) ).
iii) The area of a domain on the surface, say x(u1,u2) ((u1,u2) ∈ G), is
∫ ∫ x(G) dσ = ∫ ∫ G || xu1 ⊗ xu2 || du1du2,
where the integrand is also equal to √(a1 1 a2 2 - a1 22).
So arc length, angle and area are variables we calculate with the help of the coefficients of the first fundamental form and of variables we calculate in the u1,u2-plane ;
therefore we call them 'intrinsic variables'.
From the following definition and explanation it will become clear why we call them 'invariant under bending' as well.
Definition 108 : Consider the following picture (x1 and x2 are differentiable):
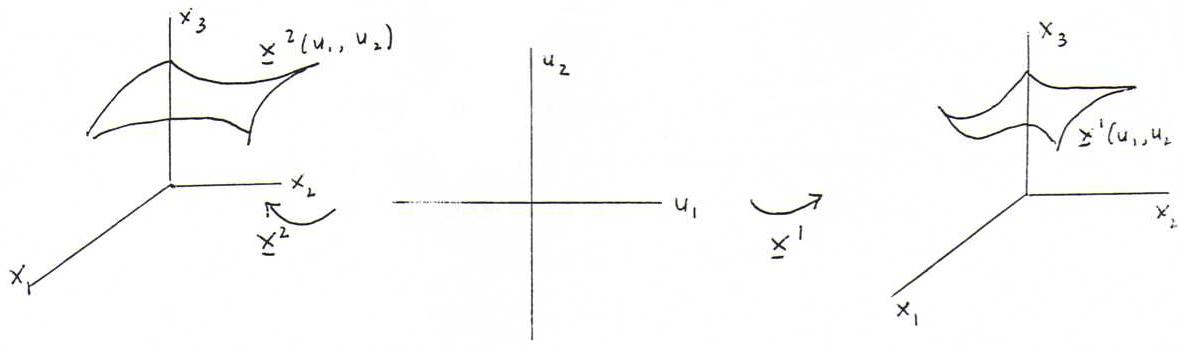
If the surfaces x1(u1,u2) and x2(u1,u2) have the same first fundamental form, we call them bents of each other, and we call the mapping x2 o (x1) -1 an isometry.
Explanation 109 : Check by calculation that the right circular cylinder x(u,v) = (cos u, sin u, v) is a bent of the plane (u,v,0);
if we shade on a piece of paper a domain and draw two curves on it, and roll up the piece of paper so that it becomes a right circular cylinder, then the area of the shaded domain, the lengths of the curves,
and the angle between the curves in the intersection point don't change.
Problem 110 : Calculate the angle between the curves (t2 cos(t3), t2 sin(t3), 2t2) and
(t3 cos(t2), t3 sin(t2), 2t3) on the surface of revolution (u cos v, u sin v, 2u) in the point with parameter value t=1.
Do this in the direct way first, and then with the help of the first fundamental form.
Problem 111 : Consider the surface V with parametrisation (u+v, u2+v2, uv). Prove that the points on V where the parameter lines are perpendicular to each other are lying on a parabola.
Problem 112 : Calculate the area of the part of the sphere with center (0,0,0) and radius 1 that lies between the parallels of latitude θ = θ1 and θ = θ2 by making use of the first fundamental form.
Problem 113 : Show that the right circular cone u(cos v, sin v, 1) (a kind of conical cap) is a bent of a plane (first use for the parametrisation of the plane polar coordinates u and v, and then make some little adaptations).