DIFFERENTIAL GEOMETRY COURSE
10. OLD EXAMINATIONS PART ONE
PROBLEM 88 : K is a curve with parameter representation ((1/2)√3 sin(t) -(1/2)t, cos(t), (1/2)sin(t) + (1/2)√3).
a) Calculate the arc length function s(t) (starting point (0,1,0)) and the curvature function κ(t).
b) Prove that the curve is a circular helix by giving the matrix of a linear mapping (here a combination of a rotation and a reflection) that transforms K into the circular helix
(cos(t), sin(t), t).
PROBLEM 89 : Calculate an equation of the sphere that has a maximal contact with the curve (t, t4, t2) in (1,1,1). (Hint:
you don't need to calculate arc length, curvature and torsion.)
PROBLEM 90 :
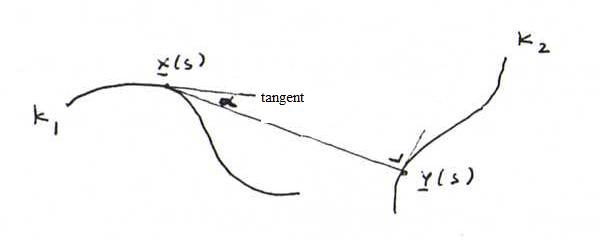
a) Suppose we have a curve K1 and a curve K2 such that with each point P1 on K1 we have a point P2 on K2
such that the binormal of K1 at P1 goes through P2 and lies in the osculating plane of K2 at P2.
Find a differential equation that must hold for the curvature function κ(s) and the torsion function τ(s) of K1 and the function λ(s) representing the distance between P1 and
P2.
b) Suppose in a) it says "rectifying plane" instead of "osculating plane". Explain which changes you have to make in your calculations. Elaborate as much as possible. What do we get if λ
is constant?
PROBLEM 91 : Let K1 be the curve with parameter representation: x(t) = (3 sin(t), 4t, 3 cos(t)).
a) Give a parametrisation of K1 with arc length s as parameter.
b) Give for each s the vectors t(s), n(s), b(s).
c) Give an equation of the plane that in x(t) has a maximal contact with K1. Elaborate!
d) Give a parametrisation of the curve K2 that lies on the same cylinder as K1 and forms with K1 a pair of curves of Bertrand.
e) What is the angle between the tangents in corresponding partner points on K1 and K2?
PROBLEM 92 : K1 is a curve with curvature κ(s) and torsion τ(s). Furthermore, we have a real number α ∈ (0,π/2).
Suppose we can choose for each s a line in the rectifying plane 'at s' making the angle α with the tangent at s and such that these lines are binormals of a curve K2.
Then what do you know about K1?
Explain your answer with calculation and reasoning. Also calculate for each s the distance between both partner points on K1 and K2.
